Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
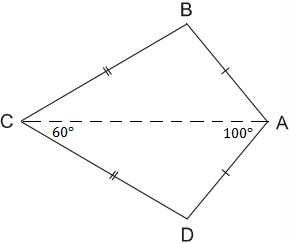
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000

Hướng dẫn cách vẽ hình : Cậu nên vẽ hình thang ABCD cân tại C và D và sao cho góc A và góc D là 2 góc kề 1 bên của tứ giác !!!!( ko bt vẽ trên này
Giải :
Ta có hình thang ABCD có 2 đáy AB và DC
=> AB//DC
Mà M là giao điểm phân giác của 2 góc B và góc D nằm trên AB
=> AM//DC
=> BM//DC
Vì AM//BC
=> AMD = MDC ( 2 góc so le trong ) ( 1)
Mà DM là pg ADC
=> ADM = MDC (2)
Từ (1) và (2) :
=> ADM = AMD
=> Tam giác AMD cân tại A
=> AD = AM(3)
Chứng minh tương tự ta cũng có tam giác MBC cân tại B và suy ra BC = MB(4)
Từ (3) và (4)
=> M là trung điểm AB
Còn ý b) ko bt làm
Sai thông cảm nhé

E, F là trung điểm của AD và BC (đề bài) => EF là đường trung bình của ht ABCD => EF//AB//CD
+ Xét tg ABD có
E là trung điểm AD (đề bài)
EI//AB
=> EI là đường trung bình của tg ABD => EI=AB/2 (1)
+ Xét tg ABC chứng minh tương tự cũng có KF=AB/2 (2)
Từ (1) và (2) => EI=KF
+ Xét tg BCD chứng minh tương tự có IF=(IK+KF)=CD/2
\(\Rightarrow IF-EI=IK+KF-EI=IK=\frac{CD}{2}-\frac{AB}{2}=\frac{CD-AB}{2}.\)
b/ Câu b dựa vào KQ của câu a

A B C D E F N I M K G
a) AM//CD. Theo định lí Ta-let, ta có: \(\frac{IM}{ID}=\frac{AI}{IC}\)( 1 )
AD//CN. Theo định lí Ta-let, ta có : \(\frac{IA}{IC}=\frac{ID}{IM}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\frac{IM}{ID}=\frac{ID}{IN}\Rightarrow ID^2=IM.IN\)
b) Ta có : \(\frac{DM}{MN}=\frac{AM}{MB}\Rightarrow\frac{DM}{DM+MN}=\frac{AM}{AM+MB}\)
do đó : \(\frac{DM}{DN}=\frac{AM}{AB}\)( 3 )
Mà ID = IK ; ID2 = IM.IN
\(\Rightarrow IK^2=IM.IN\)\(\Rightarrow\frac{IK}{IM}=\frac{IN}{IK}\Rightarrow\frac{IK-IM}{IM}=\frac{IN-IK}{IK}\)
Do đó : \(\frac{MK}{IM}=\frac{KN}{IK}\Rightarrow\frac{KM}{KN}=\frac{IM}{IK}=\frac{IM}{ID}=\frac{AM}{CD}=\frac{AM}{AB}\)( 4 )
Từ ( 3 ) và ( 4 ) suy ra \(\frac{DM}{DN}=\frac{KM}{KN}\)
c) \(\Delta AGB~\Delta AEC\left(g.g\right)\)\(\Rightarrow\frac{AB}{AG}=\frac{AC}{AE}\Rightarrow AB.AE=AC.AG=AG\left(AG+GC\right)\)( 5 )
\(\Delta BGC~\Delta CFA\left(g.g\right)\)\(\Rightarrow\frac{AF}{GC}=\frac{AC}{BC}=\frac{AC}{AD}\)
\(\Rightarrow AF.AD=AC.GC=GC\cdot\left(AG+GC\right)\)( 6 )
Cộng ( 5 ) và ( 6 ) theo vế, ta được :
\(AB.AE+AF.AD=AG\left(GC+AG\right)+GC\left(AG+GC\right)=\left(AG+GC\right)^2=AC^2\)
A M B N E C F D I G K
a/ Xét \(\Delta IMC\)có : MC // AD nên : \(\frac{IM}{ID}=\frac{IC}{IA}\)( hệ quả định lí Ta-let )
Xét \(\Delta IDC\)có : DC // AN nên : \(\frac{ID}{IN}=\frac{IC}{IA}\)( hệ quả định lí Ta-let )
Do đó : \(\frac{IM}{ID}=\frac{ID}{IN}\left(=\frac{IC}{IA}\right)\)
Vậy : \(IM.IN=ID^2\)
b/ Ta có : \(\frac{DM}{DN}=\frac{DM}{DM+MN}\)
\(=\frac{AD}{AD+NB}=\frac{AD}{CN}\)
\(=\frac{ID}{IN}=\frac{2.ID}{2.IN}\)
\(=\frac{KD}{KD+2.NK}\)
\(\Leftrightarrow\frac{DM}{DN}=\frac{KD}{DN+NK}\)
\(=\frac{KD-DM}{DN+NK-DN}=\frac{KM}{KN}\left(đpcm\right)\)
c) Xét \(\Delta ABG\)và\(\Delta ACE\)có :
\(\widehat{AGB}=\widehat{AEC}\left(=90^0\right)\)
\(\widehat{A}:chung\)
=> tam giác AGB = tam giác ACE ( cgv-gn )
\(\Rightarrow\frac{AB}{AG}=\frac{AC}{AE}\)
\(\Rightarrow AB.AE=AC.AG\)
CM tương tự,ta có : \(\Delta BCG\)đồng dạng với \(\Delta ACF\)
\(\Rightarrow\frac{BC}{GC}=\frac{AC}{AF}\)
\(\Rightarrow AC.AF=AC.GC\)
\(\Rightarrow AD.AF=AC.AG\)( vì AD = BC )
Do đó : \(AB.AE+AD.AF=AC.AG+AC.GC\)
\(\Rightarrow AB.AE+AD.AF=AC.\left(AG+GC\right)\)
\(\Rightarrow AB.AE+AD.AF=AC.AC\)
Vậy AB.AE + AD.À = AC2
Đáp án D