Tìm tích của 3 số a, b, c biết tổng của chúng, tổng các bình phương của chúng và tổng các lập phương của chúng đều bằng 1
CÁC BẠN ƠI GIÚP MÌNH CÂU NÀY VỚI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 9 2017
từ đề bài suy ra (a+b+c)^3=1suy ra (a^3)+(b^3)+(c^3)+3(a+b)(b+c)(c+a)=0 suy ra (a+b)(b+c)(c+a)=0 ( vì (a^3)+(b^3)+(c^3)=0)
nếu a+b=0 suy ra a= -b
lại có a+b+c=1 suy ra c=1
các TH còn lại CM tương tự
CM
14 tháng 12 2018
Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4
Ta có:
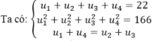
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng: 13+43+73+ 103=1408
Đáp án là D
CM
6 tháng 3 2017
Đáp án là D
Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4 và công sai là d
Ta có: u2 = u1 + d; u3= u1 + 2d; u4 = u1 + 3d
Theo giả thiết ta có:
u
1
+
u
2
+
u
3
+
u
4
=
22
u
1
2
+
u
2
2
+
u
3
2
+
u
4
2
=
166
⇔
u
1
+
u
1
+
d
+
u
1
+
2
d
+
u
1
+
3
d
=
22
u
1
2
+
(
u
1
+
d
)
2
+
(
u
1
+
2
d
)
2
+
(
u
1
+
3
d
)
2
=
166
⇔
4
u
1
+
6
d
=
22
4
u
1
2
+
12
u
1
d
+
14
d
2
=
166
⇒
2
u
1
+
3
d
=
11
(
1
)
2
u
1
2
+
6
u
1
d
+
7
d
2
=
83
(
2
)
Từ (1) suy ra: u 1 = 11 − 3 d 2 thế vào (2) ta được:
2. 11 − 3 d 2 2 + 6. 11 − 3 d 2 . d + 7 d 2 = 83 ⇔ d = 3 ⇒ u 1 = 1 d = − 3 ⇒ u 1 = 10
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng:
1 3 + 4 3 + 7 3 + 10 3 = 1408
D
1
AT
8 tháng 6 2021
gọi 2 số đó là a và b \(\left(a,b>0\right)\)
Theo đề: \(\left\{{}\begin{matrix}a+b=19\left(1\right)\\a^2+b^2=185\left(2\right)\end{matrix}\right.\)
Từ (1) \(\Rightarrow\left(a+b\right)^2=19^2=361\left(3\right)\)
Lấy \(\left(3\right)-\left(2\right)\Rightarrow2ab=176\Rightarrow ab=88\left(4\right)\)
Từ (1) và (4) \(\Rightarrow a,b\) là nghiệm của pt \(x^2-19x+88=0\)
\(\Rightarrow\left(x-11\right)\left(x-8\right)=0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=8\\b=11\end{matrix}\right.\\\left\{{}\begin{matrix}a=11\\b=8\end{matrix}\right.\end{matrix}\right.\)
Vậy 2 số cần tìm là 8 và 11
AH
Akai Haruma
Giáo viên
16 tháng 9 2023
Lời giải:
Gọi số hạng đầu tiên là $a$ và công sai $d$. Khi đó số hạng thứ 2 và 3 lần lượt là $a+d, a+2d$
Theo bài ra ta có:
$a+(a+d)+(a+2d)=12$
$\Rightarrow a+d=4$
$a^2+(a+d)^2+(a+2d)^2=66$
$\Leftrightarrow 3a^2+5d^2+6ad=66$
$\Leftrightarrow 3(4-d)^2+5d^2+6(4-d)d=66$
$\Leftrightarrow 2d^2-18=0$
$\Leftrightarrow d=\pm 3$
Nếu $d=3$ thì $a=1$. Khi đó 3 số cần tìm là $1,4, 7$
Nếu $d=-3$ thì $a=7$. Khi đó 3 số cần tìm là $7, 4, 1$
16 tháng 9 2023
\(S_3=\dfrac{3\left[2u_1+2d\right]}{2}\)
\(\Leftrightarrow2u_1+2d=\dfrac{2S_3}{3}\)
\(\Leftrightarrow2\left(u_1+d\right)=\dfrac{2S_3}{3}\)
\(\Leftrightarrow u_1+d=\dfrac{S_3}{3}=\dfrac{12}{3}=4\)
\(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_2=4\\u_3=7\end{matrix}\right.\)
mà \(u_1^2+u_2^2+u_3^2=1^2+4^2+7^2=66\) (thỏa đề bài)
Vậy 3 số hạng liên tiếp của 1 cấp số cộng là : \(1;4;7\)
21 tháng 5 2016
\(S=x^2+y^2;\)\(\frac{x^3+y^3}{x+y}=T\)
\(\Rightarrow\left(x^2+y^2\right)-\frac{x^3+y^3}{x+y}=28\)
\(\Leftrightarrow x^2+y^2-\frac{\left(x+y\right)\left(x^2-xy+y^2\right)}{x+y}=28\)
\(\Leftrightarrow xy=28\)
Vì x,y nguyên và x<y nên ta xét từng trường hợp:
- \(\hept{\begin{cases}x=-28\\y=-1\end{cases}}\)
- \(\hept{\begin{cases}x=-14\\y=-2\end{cases}}\)
- \(\hept{\begin{cases}x=-7\\y=-4\end{cases}}\)
- \(\hept{\begin{cases}x=1\\y=28\end{cases}}\)
- \(\hept{\begin{cases}x=2\\y=14\end{cases}}\)
- \(\hept{\begin{cases}x=4\\y=7\end{cases}}\)
21 tháng 5 2016
Ta được \(\left(x;y\right)=\left(-28;-1\right);\left(-14;-2\right);\left(-7;-4\right);\left(1;28\right);\left(2;14\right);\left(4;7\right)\)
NN
2
KH
3
8 tháng 6 2021
Vậy 2 số cần tìm là 8 và 11Gọi 2 số tự nhiên cần tìm là a,b (a>b)
Theo giả thiết, ta có
a + b = 19 và a^2 + b^2 = 185
=> 2ab = (a+b)^2 - (a^2+b^2) = 176 <=> ab = 88
=> a,b là nghiệm của pt x^2 - 19x + 88 = 0 (*)
(*) <=> (x-11)(x-8) = 0 <=> x= 8 hoặc x = 11
=> (a,b) = (11;8)
O
8 tháng 6 2021
gọi x là số tự nhiên thứ nhất , y là số tự nhiên thứ hai . (x,y > 0)
tổng của chúng bằng 19
=> x + y = 19
<=> x = 19 - y
tổng các bình phương của chúng bằng 185
=> x^2 + y^2 = 185
<=> (19 - y)^2 + y^2 = 185
<=> 361 - 38y + y^2 + y^2= 185
<=> 2y^2 - 38y + 176 = 0
<=> y = 8 hoặc y = 11
y = 8 => x = 19 - 8 = 11
y = 11 => x = 19 - 11 = 8
vậy hai số tự nhiên đó là 8 và 11
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2021
Gọi các số hạng của CSN là \(u_1;u_1q;u_1q^2;u_1q^3\)
\(\Rightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2+q^3\right)=15\\u_1^2\left(1+q^2+q^4+q^6\right)=85\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1^2\left(q+1\right)^2\left(q^2+1\right)^2=225\\u_1^2\left(q^2+1\right)\left(q^4+1\right)=85\end{matrix}\right.\)
\(\Rightarrow\dfrac{\left(q+1\right)^2\left(q^2+1\right)}{q^4+1}=\dfrac{45}{17}\)
\(\Leftrightarrow14q^4-17q^3-17q^2-17q+14=0\)
Với \(q=0\) ko phải nghiệm, với \(q\ne0\)
\(\Leftrightarrow14\left(q^2+\dfrac{1}{q^2}\right)-17\left(q+\dfrac{1}{q}\right)-17=0\)
\(\Leftrightarrow14\left(q+\dfrac{1}{q}\right)^2-17\left(q+\dfrac{1}{q}\right)-45=0\Rightarrow\left[{}\begin{matrix}q+\dfrac{1}{q}=-\dfrac{9}{7}\\q+\dfrac{1}{q}=\dfrac{5}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}7q^2+9q+7=0\\2q^2-5q+2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}q=2\\q=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow u_1=\dfrac{15}{1+q+q^2+q^3}=...\)
\(\hept{\begin{cases}a+b+c=1\\a^2+b^2+c^2=1\\a^3+b^3+c^3=1\end{cases}}\)
\(\left(a+b+c\right)^3=a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
- \(a+b=0\Rightarrow c=1\Rightarrow a=b=0\)
- \(b+c=0\Rightarrow a=1\Rightarrow b=c=0\)
- \(c+a=0\Rightarrow b=1\Rightarrow c=a=0\)
Vậy \(abc=0.0.1=0\)