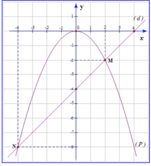
trong mặt phẳng tọa độ Oxy , gọi (d) và (l) lần lượt là đồ thị của 2 hàm số y=\(\frac{-1}{2}x\) +\(\frac{3}{2}\) và y=/x/
a, vẽ đồ thị (d) và (l) b, (d) và (l) cắt nhau tại M và N . cm tam giác OMN vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 12 2021
cảm ơn bà nha, nhưng mà tui cop sai đề nên giờ phải làm lại từ đầu
CM
13 tháng 3 2017
1) Vẽ hai đồ thị ( P ) và ( d ) trên cùng một mặt phẳng tọa độ.
* y = − 1 2 x 2 Hàm số xác định với mọi x ∈ ℝ Bảng giá trị
Nhận xét: Đồ thị hs là một parabol đi qua gốc tọa độ,nhận trục tung làm trục đối xứng nằm phía dưới trục hoành,O là điểm cao nhất *y=x-4 Đồ thị hs là đường thẳng đi qua hai điểm (0;-4) và (4;0) |
|
2)Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình
−
1
2
x
2
=
x
−
4
⇔
x
2
−
2
x
−
8
=
0
Δ ' = 1 + 8 = 9 > 0 nên phương trình có 2 nghiệm phân biệt x1=2;x2=-4
x1=2 => y1=-2 ; x2=-4 => y2=-8
Vậy tọa độ giao điểm của (P) và (d) là (2;-2) và (-4;-8)
KV
18 tháng 11 2023
a)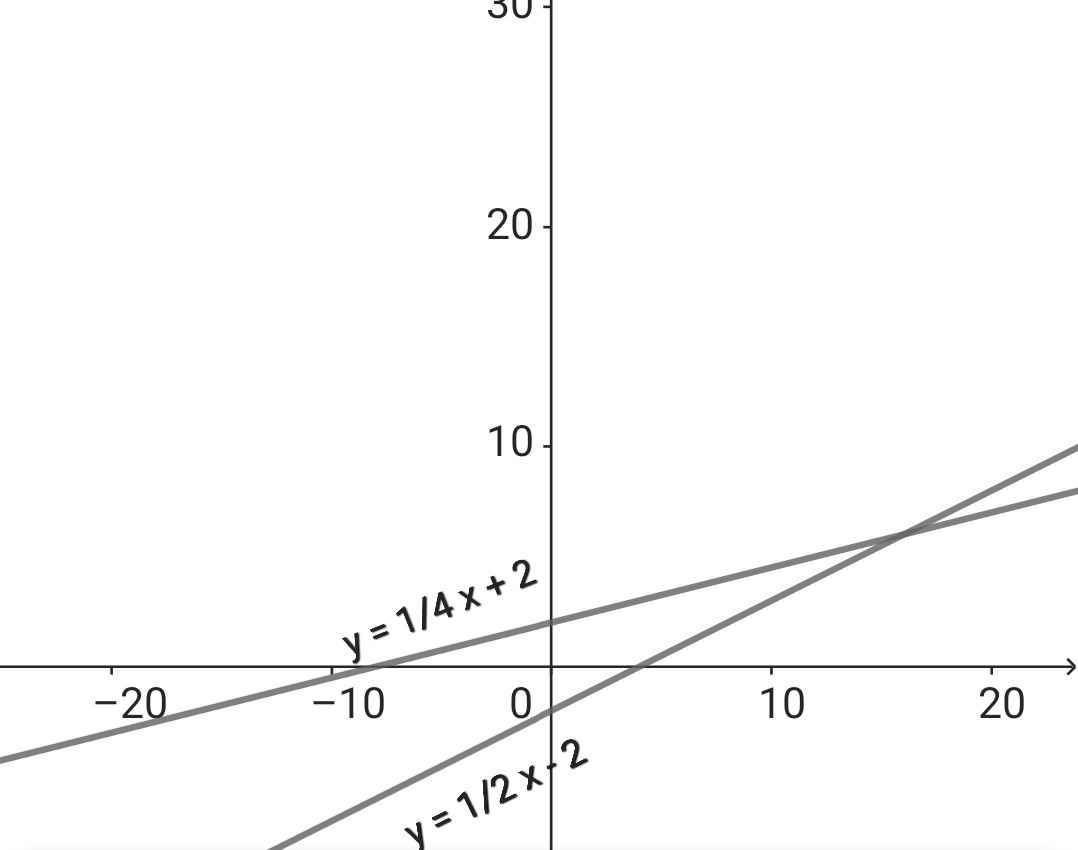 
b) *) Thay x = 0 vào (d) ta có:
y = 1/2 . 0 - 2 = -2
⇒ M(0; -2)
Thay x = 0 vào (d) ta có:
y = 1/4 . 0 + 2 = 2
⇒ N(0; 2)
Phương trình hoành độ giao điểm của (d) và (d)
1/2 x - 2 = 1/4 x + 2
⇔ 1/2 x - 1/4 x = 2 + 2
⇔ 1/4 x = 4
⇔ x = 4 : (1/4)
⇔ x = 16
Thay x = 16 vào (d) ta có:
y = 1/2 . 16 - 2 = 6
⇒ P(16; 6)
SS
13 tháng 12 2018
b/ Do (d) cắt (d) tại điểm có hoành độ = 2
=> B(2;y)
Do B(2;y) thuộc (d) => y = 2+2
=> y = 4
=> B(2;4)
Do B(2;4) thuộc (d) => 4 = (m-5)2 + m + 2
<=> 4 = 2m - 10 + m + 2
<=> 4 = 3m - 8
<=> -3m = -12
<=> m = 4
Éo ai chỉ thì tự lực cánh sinh vậy :p
27 tháng 12 2018
hoành độ giao điểm là nghiệm của phương trình:
x+2=(m-5)x+m+2 (1)
Điểm B là giao điểm có hoàng độ bằng 2 suy ra x=2
Thay x=2 vào phương trình (1) ta được
2+2=(m-5)x2+m+2 suy ra m=4
a) Đồ thị \(y=\frac{-1}{2}x+\frac{3}{2}\)có \(\hept{\begin{cases}x=0\Rightarrow y=\frac{3}{2}\\y=0\Rightarrow x=3\end{cases}}\)
Đồ thị y=|x| = \(\hept{\begin{cases}xkhix\ge0\\-xkhix\le0\end{cases}}\)
hình:.....
b) Đồ thị (D) và (L) cắt nhau tại 2 điểm có toạ độ M(1;1) và N(-3;3)
Ta có:\(OM=\sqrt{1^2+1^2}=\sqrt{2}\Rightarrow OM^2=2\)
\(ON=\sqrt{3^2+\left(-3\right)^2}=3\sqrt{2}\Rightarrow ON^2=18\)
\(MN=\sqrt{\left(1-3\right)^2+\left(1-3\right)^2}=\sqrt{20}\Rightarrow MN^2=20\)
Vì \(OM^2+ON^2=MN^2\)
Vậy tam giác OMN vuông tại O (đpcm)