Trong mặt phẳng tọa độ Oxy, cho điểm M(3;2). Có bao nhiêu đường thẳng đi qua M, cắt Ox tại điểm có hoành độ là một số nguyên dương, đồng thời cắt Oy tại một điểm có tung độ là một số nguyên dương ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 11 2018
Do điểm M’ đối xứng với điểm M qua điểm P nên P là trung điểm MM’.
Suy ra:
x P = x M + x M ' 2 y P = y M + y M ' 2 ⇔ x M ' = 2 x P − x M = 2.9 − 0 = 18 y M ' = 2 y P − y M = 2. ( − 3 ) − 4 = − 10 ⇒ M ' ( 18 ; − 10 )
Đáp án B
CM
8 tháng 8 2019
Tọa độ điểm I của đoạn thẳng MN là:
x I = x M + x N 2 = 0 + ( − 3 ) 2 = − 3 2 y I = y M + y N 2 = 4 + 2 2 = 3 ⇒ I − 3 2 ; 3
Đáp án C
CM
19 tháng 1 2019
Do P là trọng tâm tam giác MND nên:
x P = x M + x N + x D 3 y P = y M + y N + y D 3 ⇔ x D = 3 x P − x M − x N = 3.9 − 0 − ( − 3 ) = 30 y D = 3 y P − y M − y N = 3. ( − 3 ) − 4 − 2 = − 15 ⇒ D ( 30 ; − 15 )
Đáp án B
AH
Akai Haruma
Giáo viên
17 tháng 12 2021
Lời giải:
$\overrightarrow{MN}-\overrightarrow{MP}=\overrightarrow{PN}=(x_N-x_P, y_N-y_P)=(4, -3)$
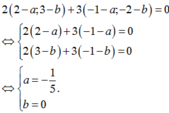
Đt qua M(3;2) có dạng y=ax+2-3a
khi x=1 thì y=2-2a. Để y nguyên dương thì có vô số giá trị a
KL: có vô số Đt thỏa mãn