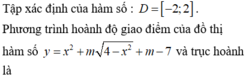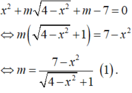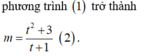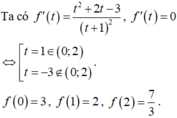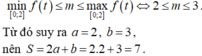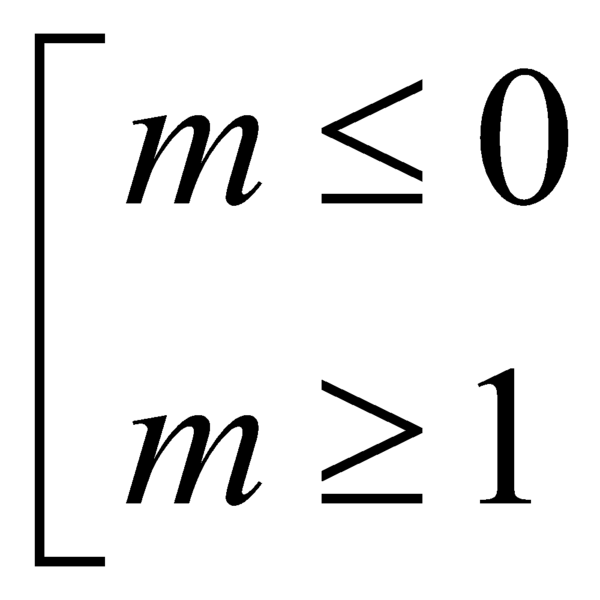tìm tất cả các giá trị của tham số m để hàm số y=x2-2x+m-1 và có trục Ox không có điểm chung
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 2 2018
Phương trình hoành độ giao điểm - x 2 - 2 x + 3 = x 2 - m
⇔ 2 x 2 + 2 x - m - 3 = 0 *
Để hai đồ thị hàm số có điểm chung khi và chỉ khi phương trình (∗) có nghiệm
⇔ ∆ = 1 - 2 - m - 3 ≥ 0 ⇔ m ≥ - 7 2
Đáp án cần chọn là: D
CM
4 tháng 8 2019
Xét phương trình hoành độ giao điểm:
x2 – 2x + m – 1 = 0 tương đương (x – 1)2 = 2 – m (1)
Để parabol không cắt trục Ox thì phương trình (1) vô nghiệm hay 2 – m < 0 hay m > 2
Chọn B.
CM
20 tháng 8 2019
Đáp án C
Phương trình hoành độ giao điểm là: m x 3 - x 2 2 x + 8 m = 0
⇔ m x + 2 x 2 - 2 x + 4 - x x + 2 = 0 ⇔ x + 2 m x 2 - 2 m x + 4 m - x = 0 ⇔ [ x = - 2 g x = m x 2 - 1 + 2 m x + 4 m = 0
Để đồ thị C m cắt trục hoành tại ba điểm phân biệt thì g x = 0 có 2 nghiệm phân biệt khác -2 ⇔ m ≠ 0 ∆ = 1 + 2 m 2 - 16 m 2 > 0 g - 2 = 4 m + 2 1 + 2 m + 4 m ≠ 0 ⇔ m ∈ - 1 6 ; 1 2 \ 0
. 
CM
24 tháng 3 2019
Đáp án C
TH1: 
suy ra 
hàm số có 
điểm cực đại 
nhận m=0.
TH2: 
.
Theo yêu cầu bài toán
.
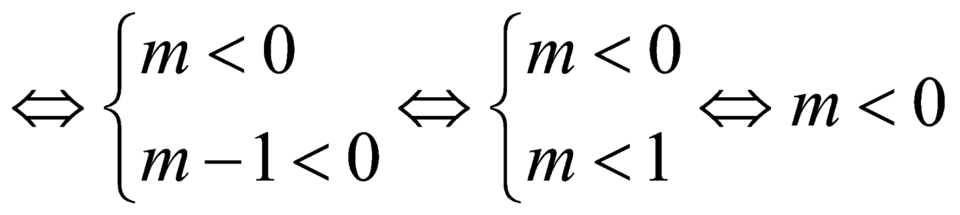Vậy 
là giá trị cần tìm.
PM
1
16 tháng 12 2021
Để hai đồ thi có điểm chung thì
\(-2x^2-2x+m+3=0\) có nghiệm
\(\Leftrightarrow4-4\cdot\left(-2\right)\left(m+3\right)>=0\)
\(\Leftrightarrow4+8m+24>=0\)
hay m>=-7/4
CM
11 tháng 9 2019
Đáp án A
Ta có y ' = x 2 − 2 x + m − 1
Đồ thị hàm số có 2 điểm cực trị đều nằm bên trái trục tung khi y ' = 0 có 2 nghiệm phân biệt đều dương
⇔ Δ ' = 1 − m + 1 > 0 S = 2 > 0 P = m − 1 > 0 ⇔ 2 > m > 1
CM
19 tháng 9 2017
Đáp án A
PT hoành độ giao điểm:
x 3 + x 2 + m = 0 ⇔ − m = x 3 + x 2 = f x
Xét hàm số: f x = x 3 + x 2 ⇒ f ' x = 3 x 2 + 2 x = 0
⇔ x = 0 ⇒ y = 0 x = − 2 3 ⇒ y = 4 27
Lập BBT hoặc vẽ đồ thị suy ra PT có đúng nghiệm
⇔ − m < 0 − m > 4 27 ⇒ m > 0 m < − 4 27 .