Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để hai đồ thi có điểm chung thì
\(-2x^2-2x+m+3=0\) có nghiệm
\(\Leftrightarrow4-4\cdot\left(-2\right)\left(m+3\right)>=0\)
\(\Leftrightarrow4+8m+24>=0\)
hay m>=-7/4

Phương trình hoành độ giao điểm - x 2 - 2 x + 3 = x 2 - m
⇔ 2 x 2 + 2 x - m - 3 = 0 *
Để hai đồ thị hàm số có điểm chung khi và chỉ khi phương trình (∗) có nghiệm
⇔ ∆ = 1 - 2 - m - 3 ≥ 0 ⇔ m ≥ - 7 2
Đáp án cần chọn là: D

Xét phương trình hoành độ giao điểm:
x2 – 2x + m – 1 = 0 tương đương (x – 1)2 = 2 – m (1)
Để parabol không cắt trục Ox thì phương trình (1) vô nghiệm hay 2 – m < 0 hay m > 2
Chọn B.

\(\left\{{}\begin{matrix}m\le x\\x\le3\end{matrix}\right.\Rightarrow m\le3\Rightarrow\left[m;3\right]\)
Vay \(m\le3\) thi ham so co tap xd la 1 doan tren truc so
P/s: Ve cai truc so ra la hieu

Pt hoành độ giao điểm:
\(\sqrt{2x^2-2x-m}-x-1=0\)
\(\Leftrightarrow\sqrt{2x^2-2x-m}=x+1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\2x^2-2x-m=x^2+2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-4x-1=m\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb \(x\ge-1\)
Từ đồ thị hàm \(y=x^2-4x-1\) ta thấy \(-5< m\le4\)

Xét phương trình hoành độ giao điểm: x2 – 2x + m – 1 = 0
Để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương thì phương trình có hai nghiệm dương hay 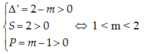
Chọn A.