Biết nghiệm dương nhỏ nhất của phương trình : \(\sqrt{3}sin2x+cos2x=1-4sinx\) có dạng \(\frac{a\pi}{b};a,b\in N^{\cdot}\) , \(\frac{a}{b}\) là phân số tối giản . Giá trị a+b bằng ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Xét phương trình \(sin\left( {x + \frac{\pi }{6}} \right) - sin2x = 0\;\)
\(\begin{array}{l} \Leftrightarrow sin\left( {x + \frac{\pi }{6}} \right) = sin2x.\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{6} = 2x + k2\pi \\x + \frac{\pi }{6} = \pi - 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Với \(x = \frac{\pi }{6} + k2\pi \) có nghiệm dương bé nhất là \(x = \frac{\pi }{6}\) khi \(k = 0\).
Với \(x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}\) có nghiệm dương bé nhất là \(x = \frac{{5\pi }}{{18}}\) khi \(k = 0\).
Vậy nghiệm dương bé nhất của phương trình đã cho là \(x = \frac{\pi }{6}\).
CM
31 tháng 12 2018
Phương trình:
3 sin 2 x + 2 sin x cos x - cos 2 x = 0 (*).
cos x = 0 ⇒ sin 2 x = 1 không phải là nghiệm của phương trình (*).
cos x ≠ 0 . Ta có:
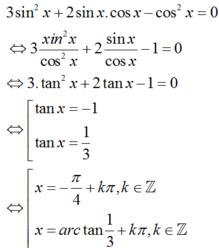
Nghiệm nguyên dương nhỏ nhất của phương trình là x 0 ∈ 0 ; π 2
Chọn C.
CM
10 tháng 1 2017
Đáp án A
Ta có 2 sin x cos x - 2 cos 2 x - 1 + sin x - cos x = 1
⇔ 2 cos x sin x - cos x + sin x - cos x = 0 ⇔ [ tan x = 1 ⇔ x = π 4 + k π cos x = - 1 2 = cos 2 π 3 ⇔ x = ± 2 π 3 + k 2 π .
17 tháng 7 2021
Pt \(\Leftrightarrow2sin\left(2x+\dfrac{\pi}{3}\right)=\sqrt{3}\)
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(x\in\left(0;\dfrac{\pi}{2}\right)\)\(\Rightarrow\left[{}\begin{matrix}0< \dfrac{\pi}{6}+k\pi< \dfrac{\pi}{2}\\0< k\pi< \dfrac{\pi}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{6}< k< \dfrac{1}{3}\\0< k< \dfrac{1}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)\(\Leftrightarrow\left[{}\begin{matrix}k=0\\k\in\varnothing\end{matrix}\right.\)
Vậy có 1 nghiệm thỏa mãn
9 tháng 9 2023
\(4sin\left(x+\dfrac{\pi}{3}\right).cos\left(x-\dfrac{\pi}{6}\right)=m^2+\sqrt[]{3}sin2x-cos2x\)
\(\Leftrightarrow4.\left(-\dfrac{1}{2}\right)\left[sin\left(x+\dfrac{\pi}{3}+x-\dfrac{\pi}{6}\right)+sin\left(x+\dfrac{\pi}{3}-x+\dfrac{\pi}{6}\right)\right]=m^2+2.\left[\dfrac{\sqrt[]{3}}{2}.sin2x-\dfrac{1}{2}.cos2x\right]\)
\(\Leftrightarrow2\left[sin\left(2x+\dfrac{\pi}{6}\right)+sin\left(2x-\dfrac{\pi}{6}\right)\right]=m^2+2\)
\(\Leftrightarrow2.2sin2x.cos\dfrac{\pi}{6}=m^2+2\)
\(\Leftrightarrow2.2sin2x.\dfrac{\sqrt[]{3}}{2}=m^2+2\)
\(\Leftrightarrow2\sqrt[]{3}sin2x.=m^2+2\)
\(\Leftrightarrow sin2x.=\dfrac{m^2+2}{2\sqrt[]{3}}\)
Phương trình có nghiệm khi và chỉ khi
\(\left|\dfrac{m^2+2}{2\sqrt[]{3}}\right|\le1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{m^2+2}{2\sqrt[]{3}}\ge-1\\\dfrac{m^2+2}{2\sqrt[]{3}}\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2\ge-2\left(1+\sqrt[]{3}\right)\left(luôn.đúng\right)\\m^2\le2\left(1-\sqrt[]{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow-\sqrt[]{2\left(1-\sqrt[]{3}\right)}\le m\le\sqrt[]{2\left(1-\sqrt[]{3}\right)}\)
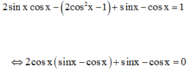
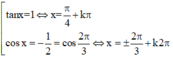
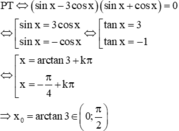
\(2\sqrt{3}sinx.cosx+1-2sin^2x=1-4sinx\)
\(\Leftrightarrow\sqrt{3}sinx.cosx-sin^2x+2sinx=0\)
\(\Leftrightarrow sinx\left(\sqrt{3}cosx-sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\\frac{1}{2}sinx-\frac{\sqrt{3}}{2}cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sin\left(x-\frac{\pi}{3}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Vậy nghiệm dương nhỏ nhất \(x=\frac{5\pi}{6}\Rightarrow a+b=11\)
Dạ ngay dấu tương đương thứ 2 thì trong ngoặc phải là +2 thì nhân vào mới là +2sinx chứ ạ