Tìm x:2x3+x-4x2-2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HM
2
19 tháng 10 2021
\(b,\Rightarrow\left(x+2\right)\left(x+2-x+3\right)=0\\ \Rightarrow5\left(x+2\right)=0\\ \Rightarrow x=-2\\ c,\Rightarrow2x\left(x^2-2x+1\right)=0\\ \Rightarrow2x\left(x-1\right)^2=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\\ d,\Rightarrow\left(x-1-2x-1\right)\left(x-1+2x+1\right)=0\\ \Rightarrow3x\left(-x-2\right)=0\\ \Rightarrow-3x\left(x+2\right)=0\\ \Rightarrow\left[{}\begin{matrix}-3x=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
H9
HT.Phong (9A5)
CTVHS
18 tháng 8 2023
\(x^6+2x^3+1=0\)
\(\Leftrightarrow\left(x^3\right)^2+2x^3+1=0\)
\(\Leftrightarrow\left(x^3+1\right)^2=0\)
\(\Leftrightarrow x^3=\left(-1\right)^3\)
\(\Leftrightarrow x=-1\)
___________
\(x\left(x-5\right)=4x-20\)
\(\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
_____________
\(x^4-2x^2=8-4x^2\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(4x^2-8\right)=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+4\left(x^2-2\right)=0\)
\(\Leftrightarrow\left(x^2-2\right)\left(x^2+4\right)=0\)
\(\Leftrightarrow x^2=2\)
\(\Leftrightarrow x=\pm\sqrt{2}\)
_______________
\(\left(x^3-x^2\right)-4x^2+8x-4\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
N
1
29 tháng 8 2023
b: 4x^2-20x+25=(x-3)^2
=>(2x-5)^2=(x-3)^2
=>(2x-5)^2-(x-3)^2=0
=>(2x-5-x+3)(2x-5+x-3)=0
=>(3x-8)(x-2)=0
=>x=8/3 hoặc x=2
c: x+x^2-x^3-x^4=0
=>x(x+1)-x^3(x+1)=0
=>(x+1)(x-x^3)=0
=>(x^3-x)(x+1)=0
=>x(x-1)(x+1)^2=0
=>\(x\in\left\{0;1;-1\right\}\)
d: 2x^3+3x^2+2x+3=0
=>x^2(2x+3)+(2x+3)=0
=>(2x+3)(x^2+1)=0
=>2x+3=0
=>x=-3/2
a: =>x^2(5x-7)-3(5x-7)=0
=>(5x-7)(x^2-3)=0
=>\(x\in\left\{\dfrac{7}{5};\sqrt{3};-\sqrt{3}\right\}\)
b) x2 – 4x +3
18 tháng 6 2023
a: P(x)=6x^3-4x^2+4x-2
Q(x)=-5x^3-10x^2+6x+11
M(x)=x^3-14x^2+10x+9
b: \(C\left(x\right)=7x^4-4x^3-6x+9+3x^4-7x^3-5x^2-9x+12\)
=10x^4-11x^3-5x^2-15x+21
CM
8 tháng 11 2018
* f(x) = x2 + 2x3− 7x5 − 9 − 6x7 + x3 + x2 + x5 − 4x2 + 3x7
= (x2+ x2 – 4x2)+ (2x3 + x3 ) - (7x5 - x5 ) – 9 – (6x7 – 3x7)
= - 2x2 + 3x3 – 6x5 – 9 – 3x7
Sắp xếp theo thứ tự tăng của biến: f(x) = −9 − 2x2 + 3x3 − 6x5 − 3x7
* g(x) = x5 + 2x3 − 5x8 − x7 + x3 + 4x2 -5x7 + x4 − 4x2 − x6 – 12
= x5+ (2x3 + x3) - 5x8 – (x7+ 5x7) + (4x2 – 4x2 ) + x4 – x6 – 12
= x5 + 3x3 – 5x8 – 6x7 + x4 – x6 – 12
Sắp xếp theo thứ tự tăng của biến: g(x) = −12 + 3x3 + x4 + x5 – x6 − 6x7− 5x8
* h(x) = x + 4x5 − 5x6 − x7 + 4x3 + x2 − 2x7 + x6 − 4x2 − 7x7 + x.
= (x+ x) +4x5 – (5x6 – x6)- (x7 + 2x7+ 7x7) + 4x3+ (x2 – 4x2)
= 2x + 4x5 - 4x6 – 10x7 + 4x3 -3x2
Sắp xếp theo thứ tự tăng của biến: h(x) = 2x − 3x2 + 4x3 + 4x5 − 4x6 − 10x7
3 tháng 10 2021
\(\dfrac{1}{2}x^2\left(2x^3-4x^2+3\right)=x^5-2x^4+\dfrac{3}{2}x^2\)
14 tháng 7 2021
Ta có: \(A=\left(x-2\right)\left(x^4+2x^3+4x^2+8x+16\right)\)
\(=x^4+2x^3+4x^2+8x+16\)
\(=3^4+2\cdot3^3+4\cdot3^2+8\cdot3+16\)
\(=81+54+36+24+16\)
\(=211\)
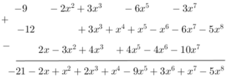
2x3 + x - 4x2 - 2 = 0
⇔ ( 2x3 - 4x2 ) + ( x - 2 ) = 0
⇔ 2x2( x - 2 ) + 1( x - 2 ) = 0
⇔ ( x - 2 )( 2x2 + 1 ) = 0
⇔ \(\orbr{\begin{cases}x-2=0\\2x^2+1=0\end{cases}}\)
+) x - 2 = 0 ⇔ x = 2
+) 2x2 + 1 = 0
⇔ 2x2 = -1 ( vô lí do 2x2 ≥ 0 ∀ x )
Vậy phương trình có nghiệm duy nhất là x = 2
\(2x^3+x-4x^2-2=0\)
\(\Leftrightarrow x\left(2x^2+1\right)-2\left(2x^2+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x^2+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\2x^2+1=0\left(loai\right)\end{cases}\Leftrightarrow}x=2\)