K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HM
2
19 tháng 10 2021
\(b,\Rightarrow\left(x+2\right)\left(x+2-x+3\right)=0\\ \Rightarrow5\left(x+2\right)=0\\ \Rightarrow x=-2\\ c,\Rightarrow2x\left(x^2-2x+1\right)=0\\ \Rightarrow2x\left(x-1\right)^2=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\\ d,\Rightarrow\left(x-1-2x-1\right)\left(x-1+2x+1\right)=0\\ \Rightarrow3x\left(-x-2\right)=0\\ \Rightarrow-3x\left(x+2\right)=0\\ \Rightarrow\left[{}\begin{matrix}-3x=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
H9
HT.Phong (9A5)
CTVHS
18 tháng 8 2023
\(x^6+2x^3+1=0\)
\(\Leftrightarrow\left(x^3\right)^2+2x^3+1=0\)
\(\Leftrightarrow\left(x^3+1\right)^2=0\)
\(\Leftrightarrow x^3=\left(-1\right)^3\)
\(\Leftrightarrow x=-1\)
___________
\(x\left(x-5\right)=4x-20\)
\(\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
_____________
\(x^4-2x^2=8-4x^2\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(4x^2-8\right)=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+4\left(x^2-2\right)=0\)
\(\Leftrightarrow\left(x^2-2\right)\left(x^2+4\right)=0\)
\(\Leftrightarrow x^2=2\)
\(\Leftrightarrow x=\pm\sqrt{2}\)
_______________
\(\left(x^3-x^2\right)-4x^2+8x-4\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
3 tháng 10 2021
\(\dfrac{1}{2}x^2\left(2x^3-4x^2+3\right)=x^5-2x^4+\dfrac{3}{2}x^2\)
14 tháng 7 2021
Ta có: \(A=\left(x-2\right)\left(x^4+2x^3+4x^2+8x+16\right)\)
\(=x^4+2x^3+4x^2+8x+16\)
\(=3^4+2\cdot3^3+4\cdot3^2+8\cdot3+16\)
\(=81+54+36+24+16\)
\(=211\)
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
a.
\(1-4x^2=\left(1-2x\right)\left(1+2x\right)\)
b.
\(8-27x^3=\left(2\right)^3-\left(3x\right)^3=\left(2-3x\right)\left(4+6x+9x^2\right)\)
c.
\(27+27x+9x^2+x^3=x^3+3.x^2.3+3.3^2.x+3^3\)
\(=\left(x+3\right)^3\)
d.
\(2x^3+4x^2+2x=2x\left(x^2+2x+1\right)=2x\left(x+1\right)^2\)
e.
\(x^2-y^2-5x+5y=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-5\right)\)
f.
\(x^2-6x+9-y^2=\left(x-3\right)^2-y^2=\left(x-3-y\right)\left(x-3+y\right)\)
20 tháng 2 2016
a)3x^3-8x^2-2x+4
=3x^3-2x^2-6x^2+4x-6x+4
=x^2(3x-2)-2x(3x-2)-2(3x-2)
=(x^2-2x-2)(3x-2).đến đây cậu tự làm nha
b)x^3-4x^2+7x-6
=x^3-2x^2-2x^2+4x+3x-6
=x^2(x-2)-2x(x-2)+3(x-2)
=(x-2)(x^2-2x+3)
.đến đây cậu tự làm nha
c)2x^3-9x+2
=2x^3-4x^2+4x^2-8x-x+2
=2x^2(x-2)+4x(x-2)-(x-2)
=(x-2)(2x^2+4x-1)
.đến đây cậu tự làm nha
AC
2
27 tháng 8 2021
\(x^4-y^4=\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
\(x^2-3y^2=\left(x-\sqrt{3}y\right)\left(x+\sqrt{3}y\right)\)
\(9\left(x-y\right)^2-4\left(x+y\right)^2=\left[3\left(x-y\right)\right]^2-\left[2\left(x+y\right)\right]^2=\left[3\left(x-y\right)-2\left(x+y\right)\right]\left[3\left(x-y\right)+2\left(x+y\right)\right]=\left(3x-3y-2x+2y\right)\left(3x-3y+2x+2y\right)=\left(x-y\right)\left(5x-y\right)\)
\(x^3+27=\left(x+3\right)\left(x^2-3x+9\right)\)
\(27x^3-0,001=\left(3x-0,1\right)\left(9x^2+0,3x+0,01\right)\)
\(125x^3-1=\left(5x-1\right)\left(25x^2+5x+1\right)\)
27 tháng 8 2021
a: \(x^4-y^4=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
c: \(9\left(x-y\right)^2-4\left(x+y\right)^2=\left(3x-3y-2x-2y\right)\left(3x-3y+2x+2y\right)=\left(x-5y\right)\left(5x-y\right)\)
d: \(\left(4x^2-4x+1\right)-\left(x+1\right)^2=\left(2x-1\right)^2-\left(x+1\right)^2\)
\(=\left(2x-1-x-1\right)\left(2x-1+x+1\right)\)
\(=3x\left(x-2\right)\)
e: \(x^3+27=\left(x+3\right)\left(x^2+3x+9\right)\)
8 tháng 1 2021
a) Ta có: \(x^3+x^2+x+1=0\)
\(\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\)
mà \(x^2+1>0\forall x\)
nên x+1=0
hay x=-1
Vậy: S={-1}
b) Ta có: \(x^3-6x^2+11x-6=0\)
\(\Leftrightarrow x^3-x^2-5x^2+5x+6x-6=0\)
\(\Leftrightarrow x^2\left(x-1\right)-5x\left(x-1\right)+6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+6\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=3\end{matrix}\right.\)
Vậy: S={1;2;3}
c) Ta có: \(x^3-x^2-21x+45=0\)
\(\Leftrightarrow x^3-3x^2+2x^2-6x-15x+45=0\)
\(\Leftrightarrow x^2\left(x-3\right)+2x\left(x-3\right)-15\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+2x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+5x-3x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2\cdot\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
Vậy: S={3;-5}
d) Ta có: \(x^4+2x^3-4x^2-5x-6=0\)
\(\Leftrightarrow x^4-2x^3+4x^3-8x^2+4x^2-8x+3x-6=0\)
\(\Leftrightarrow x^3\left(x-2\right)+4x^2\cdot\left(x-2\right)+4x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+4x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+3x^2+x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[x^2\left(x+3\right)+\left(x+1\right)\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)\left(x^2+x+1\right)=0\)
mà \(x^2+x+1>0\forall x\)
nên (x-2)(x+3)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
Vậy: S={2;-3}
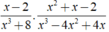
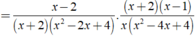
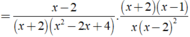
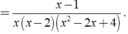
2x3 + x - 4x2 - 2 = 0
⇔ ( 2x3 - 4x2 ) + ( x - 2 ) = 0
⇔ 2x2( x - 2 ) + 1( x - 2 ) = 0
⇔ ( x - 2 )( 2x2 + 1 ) = 0
⇔ \(\orbr{\begin{cases}x-2=0\\2x^2+1=0\end{cases}}\)
+) x - 2 = 0 ⇔ x = 2
+) 2x2 + 1 = 0
⇔ 2x2 = -1 ( vô lí do 2x2 ≥ 0 ∀ x )
Vậy phương trình có nghiệm duy nhất là x = 2
\(2x^3+x-4x^2-2=0\)
\(\Leftrightarrow x\left(2x^2+1\right)-2\left(2x^2+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x^2+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\2x^2+1=0\left(loai\right)\end{cases}\Leftrightarrow}x=2\)