Cho mình hỏi cách làm toán 10 bài vecto sau
Bài 1: Cho hình bình hành ABCD tâm O. 1. Tim các vecto khác vecto không và cùng phương với nhau. 2. Tìm các vecto khác vecto không và ngược hướng với nhau.
Bài 2: Cho hình lục giác đều ABCDEF tâm O.
A. Tìm các vecto khác vecto không, cùng phương với vecto \(\overrightarrow{OA}\)
B. Tim các vecto bằng vecto \(\overrightarrow{AB}\)
C. Hãy vẽ các vecto bằng vecto \(\overrightarrow{AB}\)và có diểm đầu là O, C, D.
Bài 3: Cho hai vecto cùng phương \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\).Có thể nhận xét gì về ba điểm A, B, C
Bài 4: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh: \(\overrightarrow{NP}\) = \(\overrightarrow{MP}\), \(\overrightarrow{PQ}\) = \(\overrightarrow{MN}\)
Bài 5: Cho hình bình hành ABCD. Lấy điểm M trên đoạn AB và N trên đoạn CD sao cho AM = CN. Chứng minh: \(\overrightarrow{AN}\) = \(\overrightarrow{MC}\), \(\overrightarrow{MD}\) = \(\overrightarrow{BN}\)

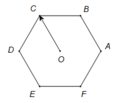
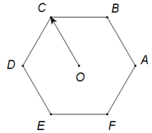
Hình bài 2
Hình bài 4
Đề bài chắc chắn sai, nhìn vào hình là thấy các vecto đó không bằng nhau