\(\sqrt{x^2-25}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: TH1: x>=2
A=x+x-2=2x-2
TH2: x<2
A=x+2-x=2
b: TH1: x>=3
A=x-3-x=-3
TH2: x<3
A=3-x-x=-2x+3
c: TH1: x>=1
C=x-x+1=1
TH2: x<1
C=x+x-1=2x-1
d: TH1: m>=3
C=m-3-2m=-3-m
TH2: m<3
C=-m+3-2m=-3m+3
e: TH1: m>=1
E=m-m+1=1
TH2: m<1
E=m+m-1=2m-1

\(\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)=\sqrt{4-2\sqrt{3}}\left(\sqrt{3}+1\right)=\sqrt{\left(\sqrt{3}-1\right)^2}\left(\sqrt{3}+1\right)\)
\(=\left|\sqrt{3}-1\right|\left(\sqrt{3}+1\right)=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)=3-1=2\)
\(\dfrac{x-25}{\sqrt{x}-5}-\dfrac{x+4\sqrt{x}+4}{\sqrt{x}+2}=\dfrac{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}{\sqrt{x}-5}-\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}+2}\)
\(=\sqrt{x}+5-\left(\sqrt{x}+2\right)=5-2=3\)
a: Ta có: \(\sqrt{2-\sqrt{3}}\cdot\left(\sqrt{6}+\sqrt{2}\right)\)
\(=\sqrt{4-2\sqrt{3}}\cdot\left(\sqrt{3}+1\right)\)
\(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\)
=3-1
=2
b: Ta có: \(\dfrac{x-25}{\sqrt{x}-5}-\dfrac{x+4\sqrt{x}+4}{\sqrt{x}+2}\)
\(=\sqrt{x}+5-\sqrt{x}-2\)
=3

Ta có
\(\left(\sqrt{25-x^2}-\sqrt{15-x^2}\right)\left(\sqrt{25-x^2}+\sqrt{15-x^2}\right)=25-x^2-15+x^2=10\)
\(\Rightarrow\sqrt{25-x^2}+\sqrt{15-x^2}=5\)

Ta có:
\(\left(\sqrt{25-x^2}-\sqrt{15-x^2}\right)\left(\sqrt{25-x^2}+\sqrt{15-x^2}\right)=25-x^2-\left(15-x^2\right)=10\)
\(\Rightarrow y=\sqrt{25-x^2}+\sqrt{15-x^2}=\dfrac{10}{2}=5\)

Ta có: \(\left(\dfrac{x-5\sqrt{x}}{x-25}-1\right):\left(\dfrac{25-x}{x+2\sqrt{x}-15}-\dfrac{\sqrt{x}+3}{\sqrt{x}+5}+\dfrac{\sqrt{x}-5}{\sqrt{x}-3}\right)\)
\(=\dfrac{x-5\sqrt{x}-x+25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}:\dfrac{25-x-x+9+x-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-5\left(\sqrt{x}-5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\cdot\dfrac{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}{-\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{5}{\sqrt{x}+3}\)

đK: \(x\ge0;x\ne25;x\ne9\)
\(=\left[\dfrac{\sqrt{x}\left(\sqrt{x}-5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}-1\right]:\left[\dfrac{25-x}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+5\right)}\right]\)
\(=\left[\dfrac{\sqrt{x}}{\sqrt{x}+5}-1\right]:\dfrac{25-x-\left(x-9\right)+\left(x-25\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-5}{\sqrt{x}+5}:\dfrac{9-x}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-5}{\sqrt{x}+5}:\dfrac{-\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)\(=\dfrac{-5}{\sqrt{x}+5}:\dfrac{-\sqrt{x}-3}{\sqrt{x}+5}\)
\(=\dfrac{-5}{\sqrt{x}+5}:\dfrac{\sqrt{x}+5}{-\left(\sqrt{x}+3\right)}=\dfrac{5}{\sqrt{x}+3}\)

ĐKXĐ: \(-5\le x\le5\)
Đề bài tương đương: \(\sqrt{\left(5-x\right)\left(5+x\right)}+x\sqrt{\left(5-x\right)\left(5+x\right)}-\left(5-x\right)=0\)
\(\Leftrightarrow\sqrt{5-x}\left(\sqrt{5+x}+x\sqrt{5+x}-\sqrt{5-x}\right)=0\)
+) \(\sqrt{5-x}=0\Leftrightarrow x=5\)
+) \(\sqrt{5+x}+x\sqrt{5+x}=\sqrt{5-x}\ge0\Rightarrow\sqrt{5+x}\left(1+x\right)\ge0\Leftrightarrow x\ge-1\)
Bình phương 2 vế của phương trình:
\(\Rightarrow\left(5+x\right)+x^2\left(5+x\right)+2x\left(5+x\right)=5-x\)
\(\Leftrightarrow x^3+7x^2+12x=0\Leftrightarrow x\left(x+3\right)\left(x+4\right)=0\)
\(\Leftrightarrow x=0;x=-3;x=-4\)Chỉ nhận \(x=0\)vì \(x\ge-1\)
\(\Rightarrow S=\left\{0;5\right\}\)

\(P=\dfrac{x-5\sqrt{x}+2x+10\sqrt{x}-3x-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}=\dfrac{5\sqrt{x}-25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}=\dfrac{5}{\sqrt{x}+5}\)
\(P=\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{2\sqrt{x}}{\sqrt{x}-5}-\dfrac{3x+25}{x-25}\\ \Leftrightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}+5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}-\dfrac{3x+25}{\left(\sqrt{x}+5\right)}\\ \Leftrightarrow P=\dfrac{x-5\sqrt{x}+2x+10\sqrt{x}-3x-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\\ \Leftrightarrow P=\dfrac{5\sqrt{x}-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\\ \Leftrightarrow P=\dfrac{5\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)
\(\Leftrightarrow P=\dfrac{5}{\sqrt{x}+5}\)
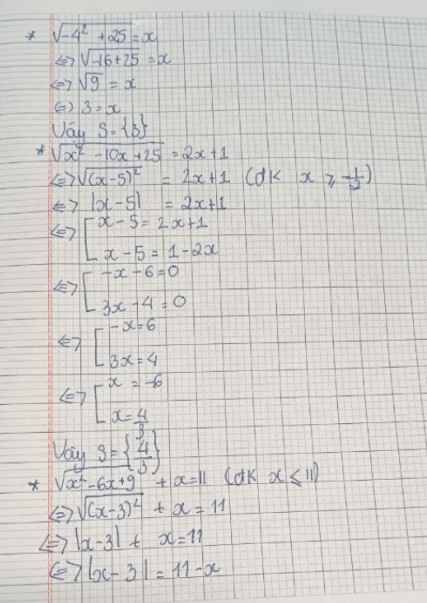
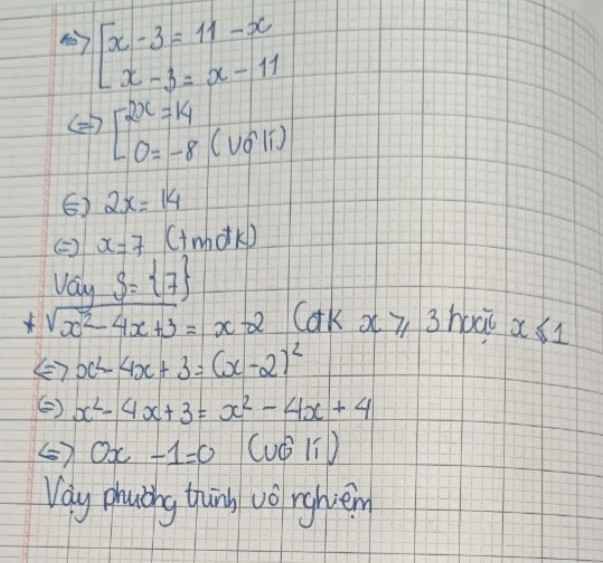
Trả lời:
\(\sqrt{x^2-25}=\sqrt{\left(x-5\right).\left(x+5\right)}\)
\(=\sqrt{x-5}.\sqrt{x+5}\)
Học tốt