Chứng minh rằng tổng của một phân số dương với nghịch đảo của nó thì không nhỏ hơn 2
Chú ý : Bài này dành cho các bạn lớp 6 nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
4
14 tháng 3 2017
nói thật thì đó là toán lớp 8, lớp 9 chứ k phải lớp 6
gọi phân số đó là a/b, vì phân số dương => a.b dương. Ta phải đi chứng minh a/b+b/a lớn hơn hoặc bằng 2
\(\frac{a}{b}+\frac{b}{a}=\frac{a^2+b^2}{ab}=\frac{a^2-ab-ab+b^2}{ab}+2=\frac{a\left(a-b\right)-b\left(a-b\right)}{ab}+2\)
\(=\frac{\left(a-b\right)^2}{ab}+2\ge2\)(vì (a-b)^2 lớn hơn hoặc bằng 0 và ab>0 => phân số đầu tiên không âm, suy ra tổng không nhỏ hơn 2)
20 tháng 3 2019
Ai chs opoke đại chiên lh mik nha! Đỏi lấy nick olm hoặc cho mik
TV
0
TT
26 tháng 3 2016
a. Gọi phân số cần tìm là \(\frac{a}{b}\)
\(\Rightarrow\) Phân số nghịch đảo là \(\frac{b}{a}\)
Theo bài ra, ta có:
\(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\Leftrightarrow\frac{a^2+b^2}{ab}\ge2\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow a^2-ab+b^2-ab\ge0\)
\(\Leftrightarrow a\left(a-b\right)+b\left(b-a\right)\ge0\)
\(\Leftrightarrow a\left(a-b\right)-b\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)
Vì (a-b)2 chắc chắn lớn hơn hoặc bằng 0
\(\Rightarrow\frac{a}{b}+\frac{b}{a}\ge2\)
Vậy tổng của một phân số dương với ghịch đảo của nó luôn lớn hơn hoặc bằng 2.
CM
2 tháng 9 2019
Gọi a/b với a > 0, b > 0 là phân số đã cho và b/a là phân số nghịch đảo của nó . Không mất tính tổng quát giả sử 0 < a ≤ b.
Đặt b = a + m (m ∈ Z, m ≥ 0)
Ta có:
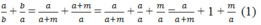
Và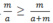 
(dấu "=" xảy ra khi m = 0)
Suy ra: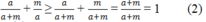 
Từ (1) và (2) suy ra:
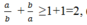, (dấu "=" xảy ra khi m = 0 hay a = b )
NT
1
2 tháng 3 2017
Giả sử phân số và nghịch đảo của nó là: \(\frac{a}{b};\frac{b}{a}\)
Do phân số dương nên( a;b) cùng dấu hay a.b>0
Ta có:
\(\frac{a}{b}+\frac{b}{a}-2=\frac{a^2+b^2-2ab}{ab}=\frac{\left(a-b\right)^2}{ab}\ge0\)
Do đó: \(\frac{a}{b}+\frac{b}{a}\ge2\)
ML
10 tháng 6 2015
Giả sử phân số và nghịch đảo của nó là \(\frac{a}{b};\frac{b}{a}\)
Do phân số dương nên \(a;b\)cùng dấu hay \(a.b>0\)
Ta có \(\frac{a}{b}+\frac{b}{a}-2=\frac{a^2+b^2-2ab}{ab}=\frac{\left(a-b\right)^2}{ab}\ge0\)
Do đó \(\frac{a}{b}+\frac{b}{a}\ge2\)
HT
15 tháng 5 2017
Gọi phân số dương là \(\dfrac{a}{b}\) . ( Không mất tính tổng quát )
Cho \(a>0,\) \(b>0\) và \(a\ge b\) . Ta có thể viết \(a=b+m\left(m\ge0\right)\) .
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{b+m}{b}+\dfrac{b}{b+m}=1+\dfrac{m}{b}\ge1+\dfrac{m}{b+m}+\dfrac{b}{b+m}=1+\dfrac{m+b}{b+m}=2\)\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{a}\ge2\)
Dấu đẳng thức xảy ra khi \(a=b\left(m=0\right)\)
(dấu "=" xảy ra khi m = 0)
, (dấu "=" xảy ra khi m = 0 hay a = b )
CK
3
LM
14 tháng 3 2016
Gọi phân số đó là a/b (ĐK: a,b # 0, a và b cùng dấu )
a/b + b/a ≥ 2 <=> (a² + b ²)/ab ≥ 2
<=> a² - 2ab + b² ≥ 0
<=> ( a – b )² ≥ 0 ( Luôn đúng với mọi a, b)
=> Đpcm
LA
19 tháng 8 2016
mk giải đc nè, tick mk nha!!
Gọi phân số dương là a/b. Ko mất tính tổng quát, giả sử như: a>0, b>0 và a > b. Ta có thể viết a=b+m ( m > 0). Ta có:
a/b+b/a=b+m/b+b/m+b=1+m/b+b/b+m > 1+ m/b+m+b/b+m=1+m+b/b+m=2.
Vậy a/b+b/a > 2.
_ Gọi phân số dương là abab (a>0;b>0)
_ Số nghịch đảo của abab là baba
Điều kiện: a≥b, a=b+m(m≥0)
Theo đề bài, ta có:
abab+ baba =b+mbb+mb +bb+mbb+m =1+mbmb +bb+mbb+m
≥ 1+mb+mmb+m +bb+mbb+m =1+m+bm+bm+bm+b
≥1+1≥2abab+baba ≥2
Vậy abab +baba ≥2
Cái này có phần hẳn hoi chứ ko phải phép tính bình thường nha! Nhưng mình lười lắm nên bạn tự phát hiện nha,có gì ko hiểu mình chỉ cho