giải bất phương trình sau:
\(x^4-5x^2+2x+3\le0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 11 2018
a) ĐKXĐ : x khác 2/5
\(\frac{2x+3}{2-5x}\le0\)
\(\Leftrightarrow2x+3\le2-5x\)
\(\Leftrightarrow7x\le-1\)
\(\Leftrightarrow x\le\frac{-1}{7}\left(\text{thỏa mãn}\right)\)
b) \(\left|5x+3\right|=\left|x+2\right|\)
\(\Rightarrow\orbr{\begin{cases}5x+3=x+2\\5x+3=-x-2\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}4x=-1\\6x=-5\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{4}\\x=\frac{-5}{6}\end{cases}}\)
P.s: cái này chưa học có j sai góp ý hộ nha ^^
7 tháng 11 2018
ĐKXĐ: \(x\ne\frac{2}{5}\)
\(\frac{2x+3}{x-5x}\le0\)
Xét 2 trường hợp
TH1: \(\hept{\begin{cases}2x+3\ge0\\2-5x< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge-\frac{3}{2}\\x>\frac{2}{5}\end{cases}}}\Leftrightarrow x>\frac{2}{5}\)
TH2: \(\hept{\begin{cases}2x+3\le0\\2-5x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le-\frac{3}{2}\\x< \frac{2}{5}\end{cases}}}\Leftrightarrow x\le-\frac{3}{2}\)
Vậy \(\orbr{\begin{cases}x>\frac{2}{5}\\x\le-\frac{3}{2}\end{cases}}\)
P/S: chưa học => trình bày thiếu sót ( sai ) => sửa hộ~
ND
Nguyễn Đức Trí
VIP
6 tháng 10 2023
Bất phương trình bậc nhất 2 ẩn :
\(2x+3y>0\Rightarrow Câu\) \(C\)
\(x-2y\le1\Rightarrow Câu\) \(f\)
\(4\left(x-1\right)+5\left(y-3\right)>2x-9\)
\(\Leftrightarrow4x-4+5y-15-2x+9>0\)
\(\Leftrightarrow2x+5y-10>0\) \(\Rightarrow Câu\) \(i\)
16 tháng 5 2023
2:
a: =>2x^2-4x-2=x^2-x-2
=>x^2-3x=0
=>x=0(loại) hoặc x=3
b: =>(x+1)(x+4)<0
=>-4<x<-1
d: =>x^2-2x-7=-x^2+6x-4
=>2x^2-8x-3=0
=>\(x=\dfrac{4\pm\sqrt{22}}{2}\)
AH
Akai Haruma
Giáo viên
25 tháng 1 2021
Lời giải:
ĐK: $x\neq -5; n\neq 0$
\(\frac{(2x+1)^4(x-3)^3}{(x+5)^2x^5}\leq 0\Leftrightarrow \left[\frac{(2x+1)^2(x-3)}{(x+5)x^2}\right]^2.\frac{x-3}{x}\leq 0\)
\(\Leftrightarrow \frac{x-3}{x}\leq 0\Rightarrow \left[\begin{matrix} x-3\geq 0; x< 0\\ x-3\leq 0; x>0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} 0> x\geq 3(\text{vô lý})\\ 3\geq x>0\end{matrix}\right.\)
Vậy $3\geq x>0$
27 tháng 2 2016
\(\Leftrightarrow\) \(\begin{cases}x\le1;2\le x\\-3\le x\le4\\x\le-2;2\le x\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}-3\le x\le-2\\2\le x\le4\end{cases}\)
Vậy hệ đã cho có tập nghiệm T = \(\left[-3;-2\right]\cup\left[2;4\right]\)
CG
1
22 tháng 2 2020
Đkxđ: \(x\ne2;x\ne3\)
Ta có \(x^2-3x+9=\left(x-\frac{3}{2}\right)^2+\frac{27}{4}\ge\frac{27}{4}>0\)
\(\Rightarrow\frac{x^2-3x+9}{x^2-5x+6}< 0\)khi và chỉ khi \(x^2-5x+6< 0\Leftrightarrow\left(x-2\right)\left(x-3\right)< 0\)
Vì \(x-2>x-3\Rightarrow\hept{\begin{cases}x-2>0\\x-3< 0\end{cases}\Rightarrow2< x< 3}\)
Vậy \(2< x< 3\)
CM
21 tháng 1 2019
a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
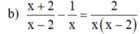
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
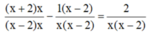
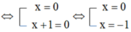
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
H
11 tháng 5 2023
`|5x| = - 3x + 2`
Nếu `5x>=0<=> x>=0` thì phương trình trên trở thành :
`5x =-3x+2`
`<=> 5x +3x=2`
`<=> 8x=2`
`<=> x= 2/8=1/4` ( thỏa mãn )
Nếu `5x<0<=>x<0` thì phương trình trên trở thành :
`-5x = -3x+2`
`<=>-5x+3x=2`
`<=> 2x=2`
`<=>x=1` ( không thỏa mãn )
Vậy pt đã cho có nghiệm `x=1/4`
__
`6x-2<5x+3`
`<=> 6x-5x<3+2`
`<=>x<5`
Vậy bpt đã cho có tập nghiệm `x<5`
\(\Leftrightarrow x^4-x^3-x^2+x^3-x^2-x-3x^2+3x+3\le0\)
\(\Leftrightarrow x^2\left(x^2-x-1\right)+x\left(x^2-x-1\right)-3\left(x^2-x-1\right)\le0\)
\(\Leftrightarrow\left(x^2+x-3\right)\left(x^2-x-1\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}\frac{-1-\sqrt{13}}{2}\le x\le\frac{1-\sqrt{5}}{2}\\\frac{-1+\sqrt{13}}{2}\le x\le\frac{1+\sqrt{5}}{2}\end{matrix}\right.\)