chứng minh rằng nếu một đường thẳng đi qua điểm A(x1;y1) và hệ số góc là a thì đường thăng đó có phương trình là y-y1=a(x-x1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử có 2 đường thẳng a và a’ đi qua A và vuông góc với d.
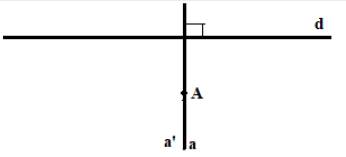
Vì a \( \bot \) d, mà a’ \( \bot \) d nên a // a’ (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Mà A \( \in \) a, A \( \in \) a'
\( \Rightarrow a \equiv a'\)
Vậy có duy nhất đường thẳng đi qua A và vuông góc với d.

Cái Này Sẽ Được Chứng Minh Ở Bài Đường Trung Bình Lớp 8, Bạn Tra Mạng Sẽ Có Nhé!

Gọi đường thẳng có dạng y = mx + n ( n khác 0 ) (1)
Vì đường thẳng cắt trục tung tại điểm b nên đt đi qua điểm có ( 0 ; b )
thay x = 0 ; y = b vào (1) ta có :
b = 0.m + n=> n = b
Vì đường thẳng cắt trục hoàng tại điểm có hoành độ là a nên dt đi qua điểm ( a; 0 )
thay x = a ; y = 0 ta có :
y = a.m + n <=> y = a.m + b => m = -b/a ( a khác 0 )
Đường thẳng đó có phương trính là \(y=\frac{-b}{a}.x+b\Leftrightarrow\frac{y}{b}=-\frac{x}{a}+1\Leftrightarrow\frac{x}{a}+\frac{y}{b}=1\)
Vậy ....

a) Thay x=-1 và y=4 vào (d), ta được:
\(3m\cdot\left(-1\right)+m-2=4\)
\(\Leftrightarrow-2m=6\)
hay m=-3
b) Để (d)//(Δ) thì \(\left\{{}\begin{matrix}3m=6\\m-2\ne-1\end{matrix}\right.\Leftrightarrow m=2\)

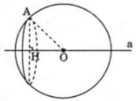
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.
Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.