Cho \(\Delta\)DBC = \(\Delta\)DEF và \(\Delta\)ABC = \(\Delta\)DFE.Chứng tỏ tam giác ABC có hai góc bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét \(\Delta ACB\) và \(\Delta EDF\) có:
\(\begin{array}{l}AC = ED\\AB = EF\\CB = DF\end{array}\)
\(\Rightarrow \Delta ACB = \Delta EDF\)(c.c.c)
Xét \(\Delta CAB\) và \(\Delta DEF\) có:
\(\begin{array}{l}CA = DE\\AB = EF\\CB = DF\end{array}\)
\(\Rightarrow \Delta CAB = \Delta DEF\)(c.c.c)
Vậy khẳng định (2) và (4) đúng.
Chú ý: Khi \(\Delta ABC = \Delta DEF\), ta cũng có thể viết \(\Delta BAC = \Delta EDF\) hay \(\Delta CBA = \Delta FED\);....

Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)
Giải:
Xem hình vẽ
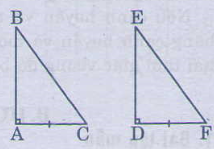
* Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)

\(\Delta ABC=\Delta DEF\Rightarrow\widehat{A}=\widehat{D},\widehat{B}=\widehat{E},\widehat{C}=\widehat{F},AB=DE,AC=DF,BC=EF\)
Ta có: ∆ABC = ∆DEF
Suy ra: AB = DE; AC = DF; BC = EF
∠A = ∠D ; ∠B = ∠E ; ∠C = ∠F

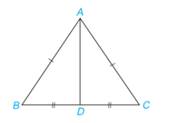
a) Xét hai tam giác ABD và ACD có:
AB=AC
AD chung
BD=DC
=>\(\Delta \)ABD = \(\Delta \)ACD (c.c.c)
b) Do \(\Delta \)ABD = \(\Delta \)ACD nên \(\widehat B = \widehat C\)( 2 góc tương ứng)

a: ΔABC và ΔEFD
Để ΔABC=ΔEFD theo trường hợp c-g-c thì BC=FD
b: ΔABC=ΔEFD
nên AB=EF=5cm; AC=ED=6cm; BC=FD=6cm
=>\(C_{ABC}=C_{EFD}=5+6+6=17\left(cm\right)\)

a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).

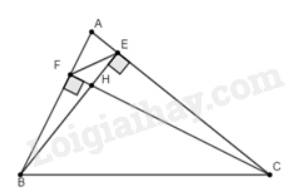
a) Vì \(BE\)là đường cao nên \(\widehat {AEB} = 90^\circ \); vì \(CF\)là đường cao nên \(\widehat {AFC} = 90^\circ \)
Xét tam giác \(AEB\) và tam giác \(AFC\) có:
\(\widehat A\) (chung)
\(\widehat {AEB} = \widehat {AFC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AEB\backsim\Delta AFC\) (g.g).
b) Vì \(\Delta AEB\backsim\Delta AFC\) nên \(\widehat {ACF} = \widehat {ABE}\) (hai góc tương ứng) hay \(\widehat {ECH} = \widehat {FBH}\).
Xét tam giác \(HEC\) và tam giác \(HFB\) có:
\(\widehat {ECH} = \widehat {FBH}\) (chứng minh trên)
\(\widehat {CEH} = \widehat {BFH} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HEC\backsim\Delta HFC\) (g.g).
Suy ra, \(\frac{{HE}}{{HF}} = \frac{{HC}}{{HB}}\) (các cặp cạnh tương ứng tỉ lệ)
Hay \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (điều phải chứng minh).
c) Xét tam giác \(HEF\) và tam giác \(HCB\) có:
\(\widehat {FHE} = \widehat {BHC}\) (hai góc đối đỉnh)
\(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (chứng minh trên)
Suy ra, \(\Delta HEF\backsim\Delta HCB\) (c.g.c).

chưa hiểu đề lắm bạn ơi
chưa sủa lại đề mà bạn