8n : 2n = 162019
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LK
1
AH
Akai Haruma
Giáo viên
10 tháng 12 2023
Lời giải:
Gọi $d=ƯCLN(2n+5, 8n+24)$
$\Rightarrow 2n+5\vdots d; 8n+24\vdots d$
$\Rightarrow 8n+24-4(2n+5)\vdots d$
$\Rightarrow 4\vdots d$ (1)
Vì $2n+5\vdots d$, mà $2n+5$ lẻ nên $d$ lẻ (2)
Từ $(1); (2)\Rightarrow d=1$
$\Rightarrow 2n+5, 8n+24$ nguyên tố cùng nhau.
$\Rightarrow BCNN(2n+5, 8n+24)=(2n+5)(8n+24)$
TS
2
1 tháng 2 2019
a, Ta có 8n - 59 = ( 2n -16 ) + ( 2n -16 ) + ( 2n - 16 ) + ( 2n - 16 ) + 5
2n - 16 luôn luôn chia hết cho 2n - 16
=> 4.(2n-16) chia hết cho 2n-16 <=> 5 chia hết cho 2n - 16
=> 2n - 16 thuộc Ư(5) = { 1;-1;5;-5 }
Tự làm nốt
b, tương tự
c, 6n - 46 = (2n-18) + (2n-18) + (2n-18) + 8
... Tiếp tục :))
TD
1 tháng 2 2019
a ,\(8n-59⋮2n-16\)
Mà \(2n-16⋮2n-16\)
\(\Rightarrow4\left(2n-16\right)⋮2n-16\)
\(\Rightarrow8n-64⋮2n-16\)
\(\Rightarrow\left(8n-59\right)-\left(8n-64\right)⋮2n-16\)
\(\Rightarrow8n-59-8n+64⋮2n-16\)
\(\Rightarrow5⋮2n-16\)
\(\Rightarrow2n-16\inƯ\left(5\right)\)
\(\Rightarrow2n-16\in\left\{\pm1;\pm5\right\}\)
\(\Rightarrow2n\in\left\{17;15;21;11\right\}\)
\(\Rightarrow\) KHÔNG CÓ SỐ NÀO THỎA MÃN CỦA 2n
\(\Rightarrow x\in\varnothing\)
KT
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2019
\(lim\left(2n-\sqrt{8n^3+8n^2+2}\right)=lim\left(2n-2n^{\frac{3}{2}}\sqrt{2+\frac{2}{n}+\frac{1}{2n^2}}\right)\)
\(=lim\left(n\left(1-2\sqrt{n}\sqrt{2+\frac{2}{n}+\frac{1}{2n^2}}\right)\right)=\infty\times\left(-\infty\right)=-\infty\)
KT
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2019
\(lim\left(2n-\sqrt[3]{8n^3+8n^2+2}\right)\)
\(=lim\frac{\left(2n-\sqrt[3]{8n^3+8n^2+2}\right)\left(4n^2+2n\sqrt[3]{8n^3+8n^2+2}+\sqrt[3]{\left(8n^3+8n^2+2\right)^2}\right)}{4n^2+2n\sqrt[3]{8n^3+8n^2+2}+\sqrt[3]{\left(8n^3+8n^2+2\right)^2}}\)
\(=lim\frac{8n^3-\left(8n^3+8n^2+2\right)}{4n^2+2n\sqrt[3]{8n^3+8n^2+2}+\sqrt[3]{\left(8n^3+8n^2+2\right)^2}}\)
\(=lim\frac{-8n^2-2}{4n^2+2n\sqrt[3]{8n^3+8n^2+2}+\sqrt[3]{\left(8n^3+8n^2+2\right)^2}}\)
\(=lim\frac{-8-\frac{2}{n^2}}{4+2\sqrt[3]{8+\frac{8}{n}+\frac{2}{n^3}}+\sqrt[3]{\left(8+\frac{8}{n}+\frac{2}{n^3}\right)^2}}\)
\(=\frac{-8+0}{4+2\sqrt[3]{8+8+0}+\sqrt[3]{\left(8+0+0\right)^2}}=\frac{-2}{3}\)
25 tháng 7 2023
\(8n+1⋮2n+1\)
\(\Rightarrow8n+1-4\left(2n+1\right)⋮2n+1\)
\(\Rightarrow8n+1-8n-4⋮2n+1\)
\(\Rightarrow-3⋮2n+1\)
\(\Rightarrow2n+1\in\left\{-1;1;-3;3\right\}\)
\(\Rightarrow n\in\left\{-1;0;-2;1\right\}\left(n\in N\right)\)
KL
1
30 tháng 11 2021
e: \(\Leftrightarrow2n+1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{0;-1;2;-3\right\}\)
NT
0
PT
1
JE
0
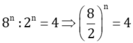
\(8^n:2^n=16^{2019}\)
\(2^{3n}:2^n=\left(2^4\right)^{2019}\)
\(2^{2n}=2^{8076}\)
\(2n=8076\)
\(n=8076:2=4038\)
\(8^n:2^n=16^{2019}\)
\(2^{3n}:2^n=\left(2^{\text{4 }}\right)^{2019}\)
\(2^{2n}=2^{8076}\)
\(2n=8076\)
\(n=4038\left(đpcm\right)\)