1. Có 6 con đường nối liền thành phố A và B và có 4 con đường hai thành phố B và C. Hỏi có bao nhiêu cách đi từ A đến C rồi từ C trở về A, cả đi và về đều phải qua B, biết rằng khi trở về không đi qua đường cũ?
A. 48
B. 576
C. 1152
D. 360
2. Từ các chữ số 0, 1, 2, 3, 5, 8 có thể lập được bao nhiêu số tự nhiên lẻ có 4 chữ số đôi một khác nhau và phải có mặt chữ số 3?
A. 36
B. 108
C. 228
D. 144

 ho bảy thành phố và các con đường nối giữa chúng như ở hình vẽ bên. hỏi từ thành phố số 1, có bao nhiêu cách đi qua tất cả các thành phố còn lại, mỗi thành phố đi qua đúng một lần, rồi quay trở về nơi xuất phát.
ho bảy thành phố và các con đường nối giữa chúng như ở hình vẽ bên. hỏi từ thành phố số 1, có bao nhiêu cách đi qua tất cả các thành phố còn lại, mỗi thành phố đi qua đúng một lần, rồi quay trở về nơi xuất phát.
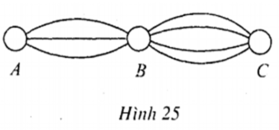
Bài 1:
Số cách đi: \(6.4.\left(6-1\right).\left(4-1\right)=360\)
Bài 2: Gọi số đó là \(\overline{abcd}\)
Số cách lập 4 chữ số lẻ bất kì: d có 3 cách chọn, a có 4, b có 4, c có 3 \(\Rightarrow3.4.4.3=144\) số
Số cách lập số lẻ ko có mặt số 3: d có 2 cách, a có 3 cách, b có 3 cách, c có 2 cách \(\Rightarrow2.3.3.2=36\) số
\(\Rightarrow\) Có \(144-36=108\) số thỏa mãn