K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
13 tháng 6 2019
Đáp án C
Số cách đi từ A đến B là 4, số cách đi từ B đến C là 2, số cách đi từ C đến D là 3.
Số cách đi từ A đến D mà qua B và C chỉ một lần là: 4.2.3 = 24 (cách)

CM
22 tháng 1 2017
Đáp án B
Nhiệt độ trung bình của thành phố Hà Nội từ 6h đến 18h là
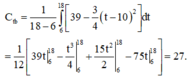


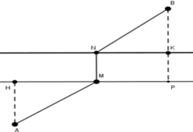

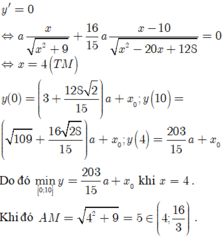
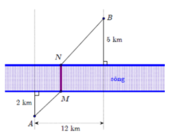


Đáp án C.
Các cách đi: A → B → D : 10 . 6 = 60 cách.
A → C → D : 9 . 11 = 99 cách.
Vậy tất cả có 159 cách đi từ A đến D.