Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án : A
Để đi từ A đến C có 6 cách chọn con đường đi từ A đến B và 4 cách chọn con đường đi từ B đến C.
Để đi từ C về A có 3 cách chọn con đường đi từ C và B và có 5 cách chọn con đường đi từ B và A (Do không đi lại các con đường đã đi rồi)
Do đó theo quy tắc nhân có:6.4.2.5 = 240 cách.

a) Để đi từ A đến D mà qua B và C chỉ một lần, phải thực hiện liên tiếp ba hành động sau đây:
Hành động 1: Đi từ A đến B. Có 4 cách để thực hiện hành động này.
Hành động 2: Đi từ B đến C. Có 2 cách để thực hiện hành động này.
Hành động 3: Đi từ C đến D. Có 3 cách để thực hiện hành động này.
Theo quy tắc nhân suy ra số các cách để đi từ A đến D mà qua B và C chỉ một lần là 4 . 2 . 3 = 24 (cách).
b) ĐS: Số các cách để đi từ A đến D (mà qua B và C chỉ một lần), rồi quay lại A (mà qua C và B chỉ một lần) là:
(4 . 2 . 3) . (3 . 2 . 4) = 242 = 576 (cách).

Có 5 cách đi từ A đến B. Đến B rồi, có 4 cách trở về A mà không đi qua con đường đã đi từ A đến B. Vậy có 5. 4 = 20 cách đi từ A đến B rồi trở về A mà không đường nào đi hai lần.

Đáp án C
Số cách đi từ A đến B là 4, số cách đi từ B đến C là 2
số cách đi từ C đến D là 3.
Số cách đi từ A đến D mà qua B và C chỉ một lần là:
4.2.3 = 24(cách)

Từ A đến B có 4 cách.
Từ B đến C có 2 cách.
Từ C đến D có 2 cách.
Vậy theo qui tắc nhân ta có 4.2.3 = 24 cách.
Chọn đáp án D.

Đáp án C.
Các cách đi: ![]() :
: ![]() cách.
cách.
![]() :
: ![]() cách.
cách.
Vậy tất cả có 159 cách đi từ A đến D.

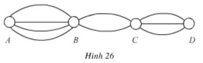
Việc đi từ A đến D là công việc được hoàn thành bởi ba hành động liên tiếp:
+ Đi từ A đến B: Có 4 con đường.
+ Đi từ B đến C: Có 2 con đường.
+ Đi từ C đến D: Có 3 con đường
⇒ Theo quy tắc nhân: Có 4.3.2 = 24 con đường đi từ A đến D mà chỉ đi qua B và C 1 lần.

a. Số cách đi từ A đến D (qua B và C chỉ một lần) là 4*3*5=60
Chọn B



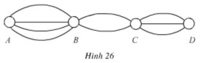

Bài 1:
Số cách đi: \(6.4.\left(6-1\right).\left(4-1\right)=360\)
Bài 2: Gọi số đó là \(\overline{abcd}\)
Số cách lập 4 chữ số lẻ bất kì: d có 3 cách chọn, a có 4, b có 4, c có 3 \(\Rightarrow3.4.4.3=144\) số
Số cách lập số lẻ ko có mặt số 3: d có 2 cách, a có 3 cách, b có 3 cách, c có 2 cách \(\Rightarrow2.3.3.2=36\) số
\(\Rightarrow\) Có \(144-36=108\) số thỏa mãn