Tìm số đo của các góc A,B,C. Biết 21*A=14*B=16*C.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2021
Ta có :
21A=14B=6C=21A42=14B42=6C42=A2=B3=C7=A+B+C2+3+7=18012=1521A42=14B42=6C42=A2=B3=C7=A+B+C2+3+7=18012=15
,mà A2=15=>A=15.2=30A2=15=>A=15.2=30
B3=15=>B=15.3=45B3=15=>B=15.3=45
C7=15=>C=15.7=105C7=15=>C=15.7=105
SUY RA GÓC A=30 ĐỘ ;GÓC B=45 ĐỘ; GÓC C=105 ĐỘ
k mik nha
10 tháng 1 2018
Theo bài ra ta có :
a + b = 24
b + c = 16
a + c = 14
=> b - a = 16 - 14 = 2
b = ( 24 + 2 ) : 2 = 13
a = 24 - 13 = 11
c = 14 - 11 = 3
Vậy a = 11 ; b = 13 ; c = 3
2 tháng 11 2016
Ta có \(\begin{cases}\frac{\widehat{A}}{3}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{5}\\\widehat{A}+\widehat{B}+\widehat{C}=180^o\end{cases}\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{5}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{3+4+5}=\frac{180^o}{12}=15\)
Suy ra \(\begin{cases}\widehat{A}=45^o\\\widehat{B}=60^o\\\widehat{C}=75^o\end{cases}\)
23 tháng 12 2020
Gọi số đo các góc A,B,C lần lượt là m,u,n
Ta có m/5=u/6=n/7 và m+u+n=180
Theo tính chất dãy tỉ bằng nhau ta có:
m/5=u/6=n/7=m+u+n/5+6+7=180/18=10
m/5=10=>m=5.10=50
u/6=10=>u=6.10=60
n/7=10=>n=7.10=70
Trả lời:
Số đo góc A là 50 độ
Số đo góc B là 60 độ
Số đo góc C là 70 độ
Cái này mik làm đại có j sai hok biết nha 🤣🤣
NT
3
XO
23 tháng 12 2019
Xét tam giác ABC có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^{\text{o}}\)
mà \(4.\widehat{A}=12.\widehat{B}=2.\widehat{C}\Rightarrow\hept{\begin{cases}4.\widehat{A}=12.\widehat{B}\\12.\widehat{B}=2.\widehat{C}\end{cases}\Rightarrow\hept{\begin{cases}\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}\\\widehat{\frac{B}{2}}=\frac{\widehat{C}}{12}\end{cases}}\Rightarrow\hept{\begin{cases}\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}\\\frac{\widehat{B}}{4}=\frac{\widehat{C}}{24}\end{cases}\Rightarrow}\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{24}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{24}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{12+4+24}=\frac{180^{\text{o}}}{40}=\frac{9^{\text{o}}}{2}\)
=> \(\hept{\begin{cases}\widehat{A}=54^{\text{o}}\\\widehat{B}=18^{\text{o}}\\\widehat{C}=108^{\text{o}}\end{cases}}\)
D
23 tháng 12 2019
Chia cả ba đẳng thức ấy cho 12 bạn sẽ được
\(\frac{4\widehat{A}}{12}=\frac{12\widehat{B}}{12}=\frac{2\widehat{C}}{12}\)
Đơn giản thì bạn sẽ có
\(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{1}=\frac{\widehat{C}}{6}\)
Theo đề ra có A+B+C=180 Vì (độ) Tổng 3 góc của một tam giác (mình không để dấu mũ ở góc với ký hiệu độ nha bạn nhớ để vào)
Áp dụng tc dãy tỉ số bằng nhau
\(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{1}=\frac{\widehat{C}}{6}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{3+1+6}=\frac{180}{10}=18\)
A=3x18=54
B=1x18=18
C=6x18=108
Vậy A=....
B=.....
C=.....
Nhớ để dấu mũ ở các góc và ký hiệu
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
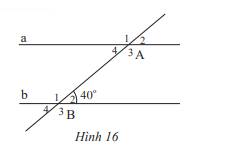
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)