
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


cả 2 phần cậu đều áp dụng tính chất dãy tỉ số bằng nhau đi
dễ mà

đề sai bạn ơi, các góc tỉ lệ chứ cạnh cđg
theo đề bài ta có :
A/3 = B/4 = C/5
=> A+B+C/3+4+5 = A/3=B/4=C/5
A+B+C = 180
=> 180/12 = A/3 = B/4 = C/5
=> 15 = A/3 = B/4 = C/5
=> A = 45 ; B = 60; C = 75
Gọi 3k, 4k, 5k lần lượt là các cạnh của tam giác ABC \(\left(k>0;k\inℝ\right)\)
Áp dụng định lí pythagore đảo vào tam giác ABC:
Vì \(\left(5k\right)^2=25k^2=9k^2+16k^2=\left(3k\right)^2+\left(4k\right)^2\)
Suy ra: tam giác ABC là tam giác vuông có độ dài cạnh huyền là 5k, độ dài 2 cạnh góc vuông là 3k, 4k
Với tam giác ABC vuông tại A, thì: \(\widehat{A}=90^0\)
Giả sử: AB = 3k ; AC = 4k
\(\sin B=\frac{AC}{BC}=\frac{4k}{5k}=\frac{4}{5}\Rightarrow\widehat{B}\approx53^0\)
Vì tổng các góc \(\widehat{A}=90^0\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^0\)
\(\Rightarrow\widehat{C}=90^0-\widehat{B}=90^0-53^0=37^0\)
Vậy 3 góc trong tam giác có số đo là: \(90^0;37^0;53^0\)
HỌC TỐT!

Gọi các góc của \(\Delta ABC\) là :a,b,c
a, Ta có : \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4};a+b+c=180^o\)
Áp dụng t/c dtsbn , ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180^o}{9}=20^o\)
\(\Rightarrow\left\{{}\begin{matrix}a=40^o\\b=60^o\\c=80^o\end{matrix}\right.\)
\(\Rightarrow\)Số đo các góc của \(\Delta ABC:....\)
b,Ta có : \(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3};a+b+c=180^o\)
Áp dụng t/c dtsbn , ta có :
\(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3}=\dfrac{a+b+c}{1+2+3}=\dfrac{180^o}{6}=30^o\)
\(\Rightarrow\left\{{}\begin{matrix}a=30^o\\b=60^o\\c=90^o\end{matrix}\right.\)
\(\Rightarrow\)Số đo các góc của \(\Delta ABC\):...
Gọi số đo ba góc của tg lần lượt là: \(a,b,c\left(a,b,c>0\right)\)
Áp dụng t/c dtsbn:
a. \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180^0}{9}=20\)
\(\Rightarrow\left\{{}\begin{matrix}a=40^0\\b=60^0\\c=80^0\end{matrix}\right.\)
câu b lm tương tự nhé!

Ta có :
\(\widehat{A}=12+\widehat{C}\)
\(\widehat{B}=6+\widehat{C}\)
Xét tam giác ABC có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180\)
=> \(12+\widehat{C}+6+\widehat{C}+\widehat{C}=180\)
=> \(18+3\widehat{C}=180\)
=> \(3\widehat{C}=162\)=> \(\widehat{C}=54^o\)
=> \(\widehat{A}=12+\widehat{C}=12+54=66^o\)
\(\widehat{B}=6+\widehat{C}=6+54=60^o\)
A - C = 12 (1)
B - C = 6 (2)
( tổng 3 góc của 1 tam giác ) có : A + B + C = 180 (3) ( tổng 3 góc của 1 tam giác )
Lấy (3) - (1) ta có :
A + B + C - A + C = 180 - 12
<=> B + 2C = 168 (4)
Lấy (4) - (2) ta có :
B + 2C - B + C = 168 - 6
3C = 162
C = 54
=> A = 54 + 12 = 66
=> B = 180 - 54 - 66 = 60
Vậy A = 66; B = 60; C = 54

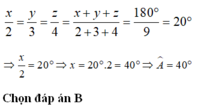
Xét tam giác ABC có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^{\text{o}}\)
mà \(4.\widehat{A}=12.\widehat{B}=2.\widehat{C}\Rightarrow\hept{\begin{cases}4.\widehat{A}=12.\widehat{B}\\12.\widehat{B}=2.\widehat{C}\end{cases}\Rightarrow\hept{\begin{cases}\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}\\\widehat{\frac{B}{2}}=\frac{\widehat{C}}{12}\end{cases}}\Rightarrow\hept{\begin{cases}\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}\\\frac{\widehat{B}}{4}=\frac{\widehat{C}}{24}\end{cases}\Rightarrow}\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{24}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{\widehat{A}}{12}=\frac{\widehat{B}}{4}=\frac{\widehat{C}}{24}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{12+4+24}=\frac{180^{\text{o}}}{40}=\frac{9^{\text{o}}}{2}\)
=> \(\hept{\begin{cases}\widehat{A}=54^{\text{o}}\\\widehat{B}=18^{\text{o}}\\\widehat{C}=108^{\text{o}}\end{cases}}\)
Chia cả ba đẳng thức ấy cho 12 bạn sẽ được
\(\frac{4\widehat{A}}{12}=\frac{12\widehat{B}}{12}=\frac{2\widehat{C}}{12}\)
Đơn giản thì bạn sẽ có
\(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{1}=\frac{\widehat{C}}{6}\)
Theo đề ra có A+B+C=180 Vì (độ) Tổng 3 góc của một tam giác (mình không để dấu mũ ở góc với ký hiệu độ nha bạn nhớ để vào)
Áp dụng tc dãy tỉ số bằng nhau
\(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{1}=\frac{\widehat{C}}{6}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{3+1+6}=\frac{180}{10}=18\)
A=3x18=54
B=1x18=18
C=6x18=108
Vậy A=....
B=.....
C=.....
Nhớ để dấu mũ ở các góc và ký hiệu