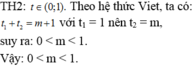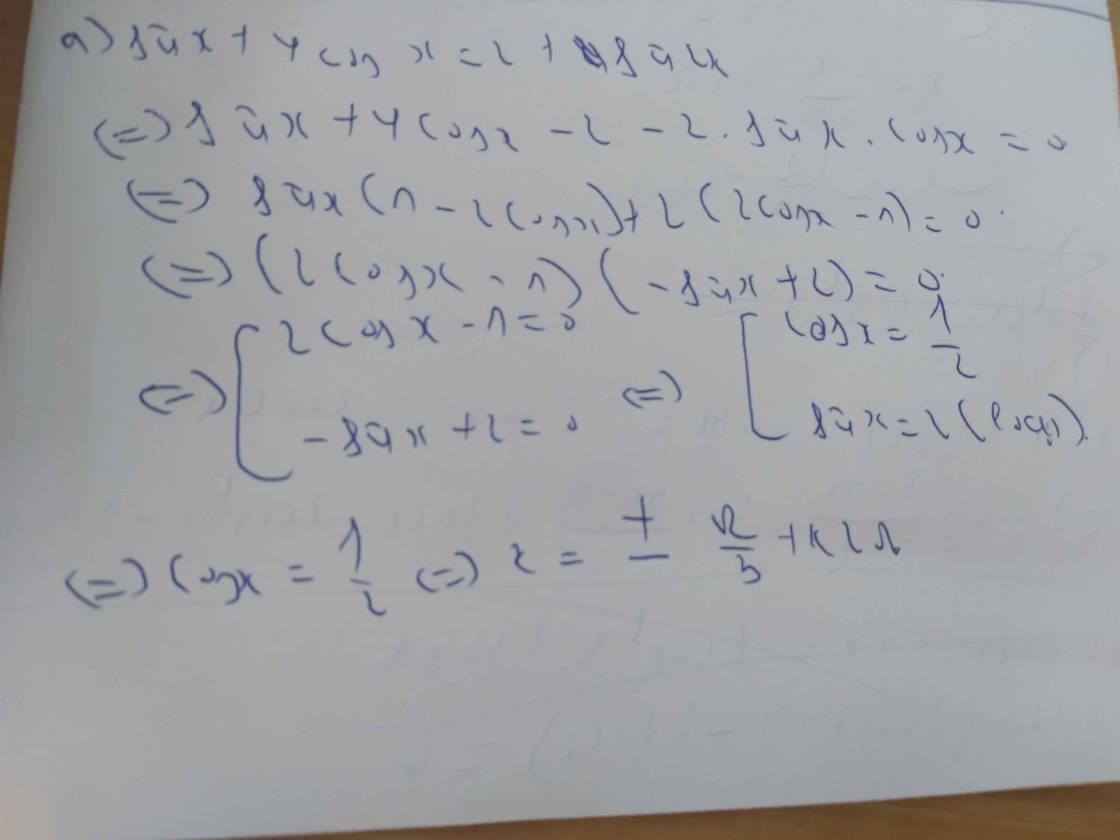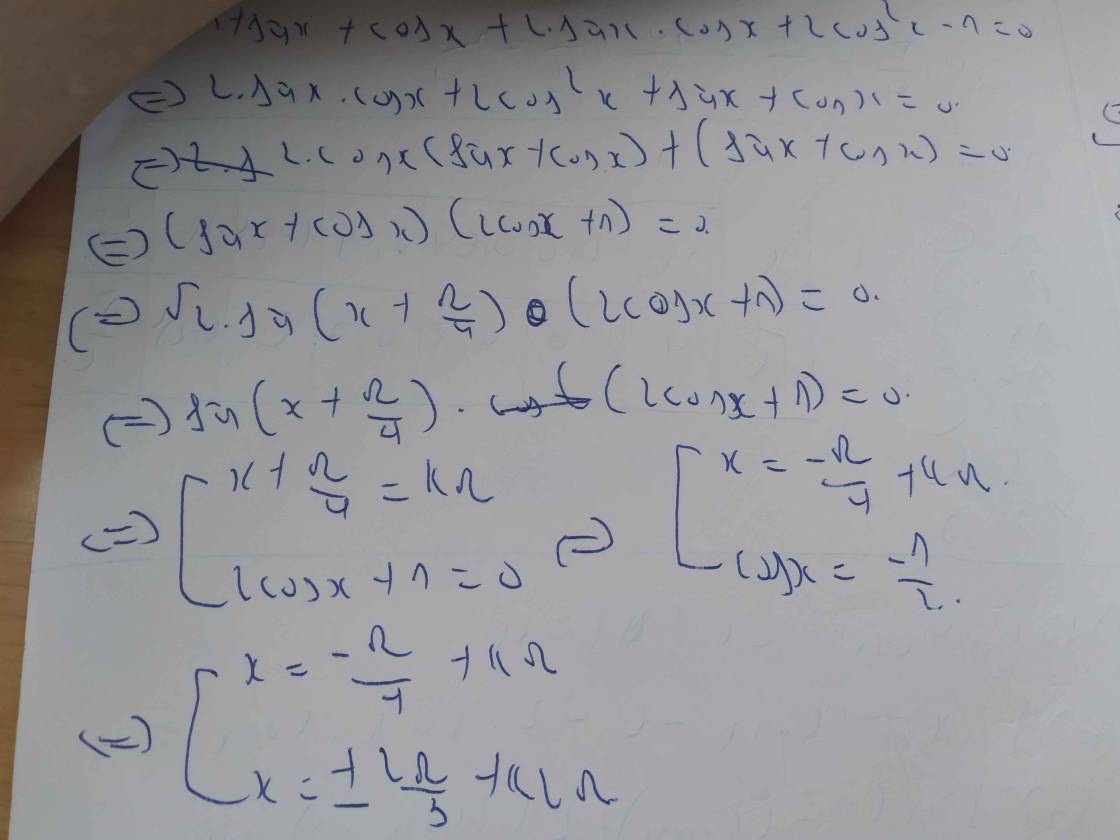Sĩn*sin2x=1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong khoảng đã cho \(tanx\) luôn dương nên ko cần tìm ĐKXĐ
\(\Leftrightarrow1+sinx+cosx+sin2x+cos2x=0\)
\(\Leftrightarrow sinx+cosx+2sinx.cosx+2cos^2x=0\)
\(\Leftrightarrow sinx+cosx+2cosx\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2cosx+1\right)=0\)
Do \(0< x< \frac{\pi}{2}\Rightarrow\left\{{}\begin{matrix}sinx>0\\cosx>0\end{matrix}\right.\)
\(\Rightarrow\left(sinx+cosx\right)\left(2cosx+1\right)>0\)
Pt vô nghiệm trên \(\left(0;\frac{\pi}{2}\right)\)
Giải phương trình: \(\frac{cosx\left(cosx+2sinx\right)+3sinx\left(sĩn+\sqrt{2}\right)}{2sinx-1}\)= 1

Cái chỗ biến đổi tương đương cuối cùng bạn làm rõ chút dc ko???
Ném đoạn \(2sin^2x+\left(3\sqrt{2}-2\right)sinx+1\) vào casio mà bấm pt bậc 2 thôi, nó sẽ tách ra biểu thức như cái cuối cùng
Hoặc là tách thế này:
\(2sin^2x+\left(3\sqrt{2}-2\right)sinx+1\)
\(=2\left[sin^2x-2.\frac{2-3\sqrt{2}}{4}sinx+\left(\frac{2-3\sqrt{2}}{4}\right)^2-\left(\frac{2-3\sqrt{2}}{4}\right)^2\right]+1\)
\(=2\left(sinx-\frac{2-3\sqrt{2}}{4}\right)^2-2\left(\frac{2-3\sqrt{2}}{4}\right)^2+1\)
\(=2\left(sin^2x-\frac{2-3\sqrt{2}}{4}\right)^2+\frac{6\sqrt{2}-7}{4}\)
Với lưu ý \(\frac{6\sqrt{2}-7}{4}>0\) nên biểu thức luôn dương

Đặt \(t=sinx\) , \(-1\le t\le1\)
Phương trình đã cho trở thành:
\(4t^2-2\left(\sqrt{3}+1\right)t+\sqrt{3}=0\)
\(\Leftrightarrow\left(2t-1\right)\left(2t-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{1}{2}\\t=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\) (nhận)
+ Với \(sinx=\dfrac{1}{2}\Rightarrow sinx=sin\dfrac{\pi}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
+ Với \(sinx=\dfrac{\sqrt{3}}{2}\Rightarrow sinx=sin\dfrac{\pi}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
Vậy ....

Bạn tham khảo:
Có bao nhiêu nghiệm nguyên m để hàm số f(x)= m(2020 x-2cosx) sinx -x nghịch biến trên R A .vô số B.2 C.1 D.0 - Hoc24

ngại viết quá hihi, mà hơi ngáo tí cái dạng này lm rồi mà cứ quên
bài trước mk bình luận bạn đọc chưa nhỉ

\(P=\frac{cosx+\sqrt{3}sinx}{\sqrt{3}cosx-sinx}=\frac{\frac{1}{2}cosx+\frac{\sqrt{3}}{2}sinx}{\frac{\sqrt{3}}{2}cosx-\frac{1}{2}sinx}=\frac{sin\left(\frac{\pi}{6}\right).cosx+cos\left(\frac{\pi}{6}\right).sinx}{cos\left(\frac{\pi}{6}\right).cosx-sin\left(\frac{\pi}{6}\right).sinx}\)
\(P=\frac{sin\left(\frac{\pi}{6}+x\right)}{cos\left(\frac{\pi}{6}+x\right)}=tan\left(\frac{\pi}{6}+x\right)\)

\(\frac{1-sin2x}{1+sin2x}=\frac{sin^2x+cos^2x-2sinx.cosx}{sin^2x+cos^2x+2sinx.cosx}=\frac{\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}\)
\(=\frac{\left[\sqrt{2}sin\left(x-\frac{\pi}{4}\right)\right]^2}{\left[\sqrt{2}.sin\left(x+\frac{\pi}{4}\right)\right]^2}=tan^2\left(\frac{\pi}{4}-x\right)\)
Bạn coi lại đề, vế phải là tan chứ ko phải cot
\(\frac{sin2x-2sinx}{sin2x+2sinx}=\frac{2sinx.cosx-2sinx}{2sinx.cosx+2sinx}=\frac{2sinx\left(cosx-1\right)}{2sinx\left(cosx+1\right)}\)
\(=\frac{cosx-1}{cos+1}=\frac{1-2sin^2\frac{x}{2}-1}{2cos^2\frac{x}{2}-1+2}=\frac{-2sin^2\frac{x}{2}}{2cos^2\frac{x}{2}}=-tan^2\frac{x}{2}\)