2sin6x – 3cos4x + 1 = 3sin4x – 2cos6x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(\left\{{}\begin{matrix}sin^2x+cos^2x=1\\4sin^4x+3cos^4x=\dfrac{7}{4}\end{matrix}\right.\)
\(\Rightarrow4sin^4x+3\left(1-sin^2x\right)^2=\dfrac{7}{4}\)
\(\Leftrightarrow7sin^4x-6sin^2x+\dfrac{5}{4}=0\) \(\Rightarrow\left[{}\begin{matrix}sin^2x=\dfrac{1}{2}\Rightarrow cos^2x=\dfrac{1}{2}\\sin^2x=\dfrac{5}{14}\Rightarrow cos^2x=\dfrac{9}{14}\end{matrix}\right.\)
Do đó: \(\left[{}\begin{matrix}A=\dfrac{7}{4}\\A=\dfrac{57}{28}\end{matrix}\right.\)

Nhận thấy \(sinx=0\) ko phải nghiệm
\(\Leftrightarrow sinx\left(2cos2x+1\right)\left(2cos6x+1\right)\left(2cos18x+1\right)=sinx\)
\(\Leftrightarrow\left(2cos2x.sinx+sinx\right)\left(2cos6x+1\right)\left(2cos18x+1\right)=sinx\)
\(\Leftrightarrow\left(sin3x-sinx+sinx\right)\left(2cos6x+1\right)\left(2cos18x+1\right)=sinx\)
\(\Leftrightarrow\left(2cos6x.sin3x+sin3x\right)\left(2cos18x+1\right)=sinx\)
\(\Leftrightarrow\left(2cos18x.sin9x+sin9x\right)=sinx\)
\(\Leftrightarrow sin27x=sinx\)

\(sinx\left(1+2cos2x+2cos4x+2cos6x\right)\)
\(=sinx+2sinx.cos2x+2sinx.cos4x+2sinx.cos6x\)
\(=sinx+sin3x+sin\left(-x\right)+sin5x+sin\left(-3x\right)+sin7x+sin\left(-5x\right)\)
\(=sinx+sin3x-sinx+sin5x-sin3x+sin7x-sin5x\)
\(=sin7x\)

\(PT\Leftrightarrow\left\{{}\begin{matrix}sin3x+cos3x>=0\\2\cdot\left(sin3x+cos3x\right)^2=1+2\cdot sin6x+2\cdot sin2x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}sin3x+cos3x>=0\\2+2\cdot sin6x=1+2\cdot sin6x+2\cdot sin2x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}sin3x+cos3x>=0\left(1\right)\\sin2x=\dfrac{1}{2}\left(2\right)\end{matrix}\right.\)
(2): sin2x=1/2
=>2x=pi/6+k2pi hoặc 2x=5/6pi+k2pi
=>x=pi/12+kpi hoặc x=5/12pi+kpi
Khi x=pi/12+kpi thì:
\(sin3x+cos3x=sin\left(\dfrac{pi}{4}+3\cdot kpi\right)+cos\left(\dfrac{pi}{4}+3\cdot kpi\right)\)
Để sin 3x+cos3x>=0 thì k=2n
Khi x=5/12pi+kpi thì \(sin3x+cos3x=sin\left(\dfrac{5}{4}pi+3\cdot kpi\right)+cos\left(\dfrac{5}{4}pi+3\cdot k\cdot pi\right)\)
Để sin 3x+cos3x>=0 thì \(k=2n+1\)
=>Phương trình ban đầu sẽ có các nghiệm là: \(x=\dfrac{pi}{12}+2npi;x=\dfrac{17}{12}pi+2npi\)

`2+2cos6x-5cos3x=-3`
`<=>2(cos^2 3x-1)-5cos3x+5=0`
`<=>2cos^2 3x -5cos3x-3=0`
Đặt `t=cos3x (-1 <=t<=1)`, ta có PT:
`2t^2-5t-3=0`
`<=>[(t=3\ (L)),(t=-1/2):}`
Với `t=-1/2`, có: `cos3x=-1/2`
`<=>3x= pm (2\pi)/3 +k2\pi`
`<=>x=\pm (2\pi)/9 +k (2\pi)/3\ (k in ZZ)`
Vậy PT có 2 họ nghiệm như trên.

\(6sinx.cos4x+4sin^2x-8sinx+3cos4x+2sinx-4+4cos^2x=3\)
\(\Leftrightarrow6sinx.cos4x-6sinx+3cos4x-3=0\)
\(\Leftrightarrow cos4x\left(2sinx+1\right)-\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(cos4x-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)

M = 3(sin^8x-cos^8x) + 4(cos^6x-2sin^6x)+6sin^4x
Ta có:
sin^8(x) - cos^8(x) = [sin^4(x) ]² - [cos^4(x)]²
= (sin²x + cos²x)(sin²x -cos²x).[ sin^4(x) + cos^4(x) ]
= (sin²x -cos²x)[ sin^4(x) + cos^4(x) ]
= sin^6(x) - cos^6(x) + sin²x.cos^4(x) -cos²x.sin^4(x)
Lúc đó M viết lại là:
M = 3.[sin^6(x) - cos^6(x) + sin²x.cos^4(x) -cos²x.sin^4(x) ] + 4.[ cos^6(x) -2sin^6(x) ] + 6sin^4(x)
M = -5sin^6(x) + cos^6(x) -3sin^4(x).cos²x + 3sin²x.cos^4(x) +6sin^4(x)
M = -3sin^(6)x - 3cos²x.sin^4(x) + cos^4(x).sin²x + cos^6(x) - 2sin^6(x) + 2sin²x.cos^4(x) + 6sin^4(x)
M = -3sin^4(x).(sin²x + cos²x ) + cos^4(x).[sin²x + cos²x ] -2sin²x.[sin^4(x) - cos^4(x) ] + 6sin^4(x)
M = 3sin^4(x) + cos^4(x) -2sin²x.[sin²x - cos²x]
M = 3sin^4(x) + cos^4(x) -2sin^4(x) + 2sin²x.cos²x
M = sin^4(x) + 2sin²x.cos²x + cos^4(x)
M = [sin²x + cos²x ]² = 1
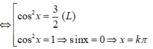
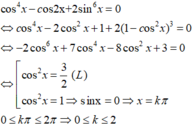
\(VT=2sin^6x-3cos^4x+1=2sin^6x+2cos^6x-3cos^4x-3sin^4x+1+3sin^4x-2cos^6x\)
Dài quá, không đủ viết chung 1 dòng, tách lẻ ra:
\(2\left(sin^6x+cos^6x\right)=2\left[\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\right]\)
\(=2-6sin^2x.cos^2x\)
\(-3\left(sin^4x+cos^4x\right)=-3\left(sin^2x+cos^2x\right)^2+6sin^2x.cos^2x\)
\(=-3+6sin^2x.cos^2x\)
\(\Rightarrow VT=2-6sin^2x.cos^2x-3+6sin^2x.cos^2x+1+3sin^4x-2cos^6x\)
\(=3sin^4x-2cos^6x\)