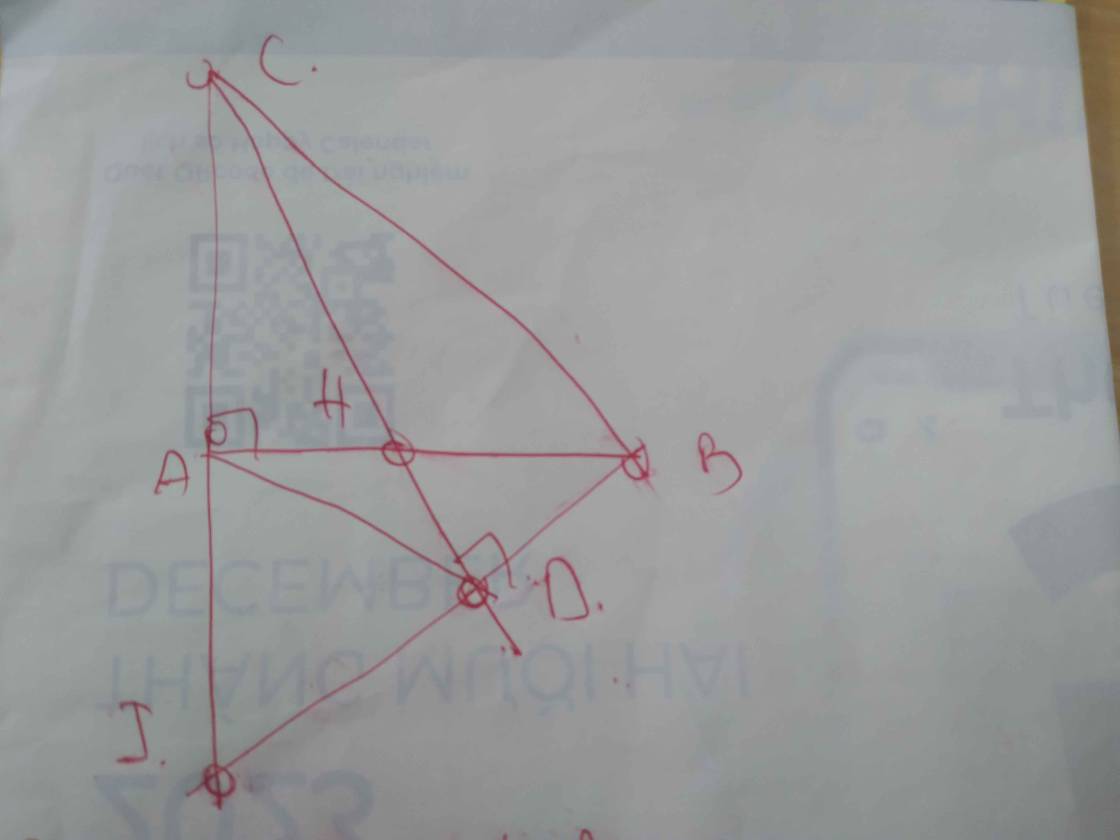
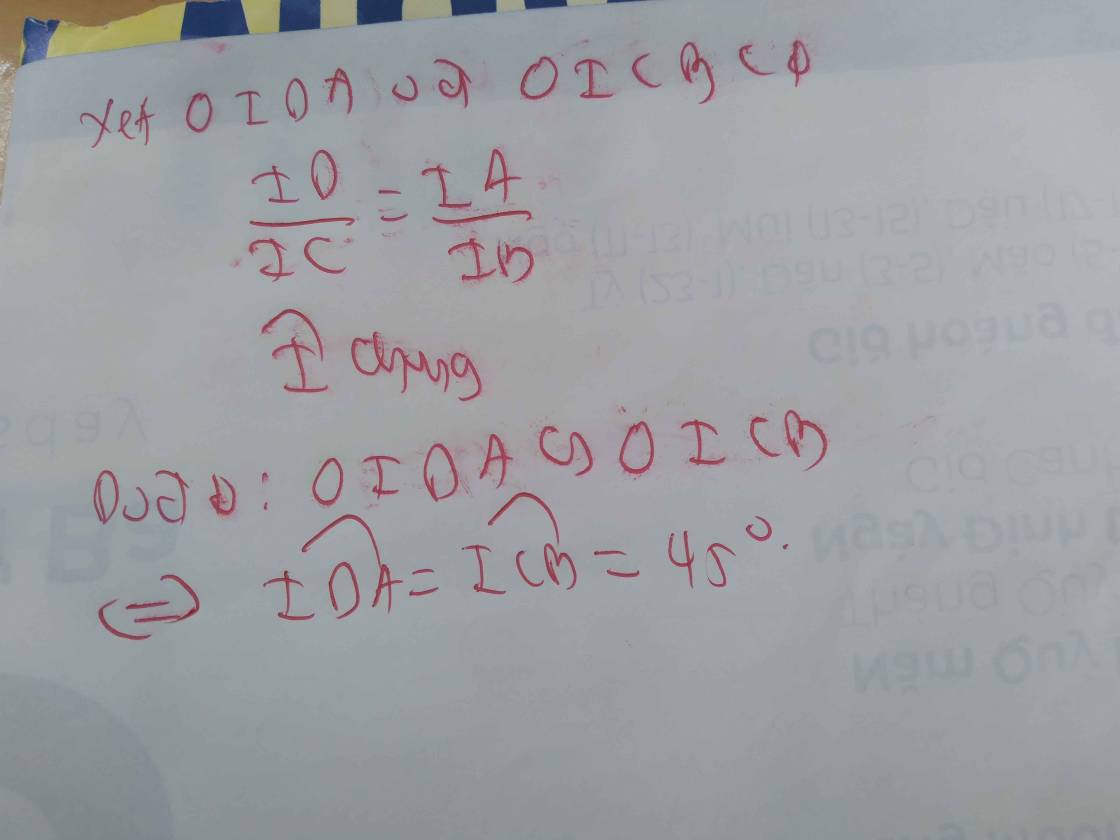cho tam giác vuông cân MNP vuông tại M. trên MN lấy điểm k, vẽ qua N đường thẳng d vuông góc với đường P thẳng K tại R và đường thẳng PM tại I
a)chứng minh IR.IN=IM.TP
b) chứng minh NR.NI+PM.PI=NP2
c) tính góc IRM
vẽ tia phân giác cua goc IMR cắt IR tại T. chứng minh MT2<MI.MR
bài này tìm trên mạng ko có nha các bn