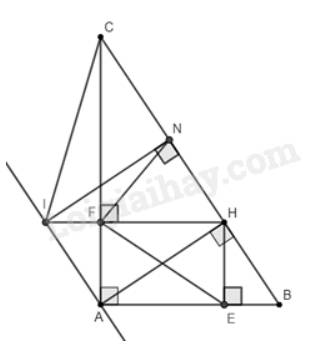
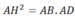Cho $\Delta ABC$vuông tại A (AB

NQ

Nguyễn Quốc Huy

14 tháng 2 2019 - olm

Cho $\Delta ABC$vuông tại A (AB<AC), đường cao AH. Đường tròn tâm I đường kính AH cắt các cạnh AB, AC lần lượt tại M, N. Gọi O là trung điểm BC, D là giao của OA và MN.a/ Chứng minh AM.AB=AN.AC và tứ giác BMNC nội tiếpb/ Chứng minh: $\Delta ADI$đồng dạng với$\Delta AHO$ và $\frac{1}{AD}=\frac{1}{HB}+\frac{1}{HC}$c/ Gọi P là giao điểm của BC và MN, K là giao điểm thứ 2 của AP và đường tròn đường kính...

Đọc tiếp

#Toán lớp 9

0

QT

Quyên Teo

29 tháng 10 2021

Ôn tập:1. Tìm x, y:2. Cho $\Delta$DMN vuông tại M, biết $\widehat{D}$= 37$^o$ và DN= 10cm. Giải tam giác vuông DMN?3. Cho $\Delta$ABC $\perp$ tại B, AB= 8cm, $\widehat{A}$= 53$^o$....

Đọc tiếp

#Toán lớp 9

1

I

ILoveMath

29 tháng 10 2021

a) Áp dụng HTL ta có:$MH.HP=MH^2\Rightarrow x=\sqrt{2.8}=4$

$BC=MH+HP=10$

Áp dụng HTL ta có: $HP.NP=MP^2\Rightarrow y=\sqrt{8.10}=4\sqrt{5}$

b) Áp dụng HTL ta có: $EQ.QF=DQ^2\Rightarrow x=\dfrac{4^2}{1}=16$

$EF=EQ+QF=17$

Áp dụng HTL ta có: $QP.EF=y^2\Rightarrow y=\sqrt{17.1}=\sqrt{17}$

Đúng(2)

TN

Thanh Nhã Phạm

19 tháng 3 2023

cho $\Delta$ABC có AB<AC vuông tại B, phân giác AD của góc A cắt BC tại D. từ D kẻ DH vuông góc với AC (H∈AC);và HD và AB kéo dài cắt tai I. Chứng minh rằng:a) $\Delta$ABC = $\Delta$AHD b) AD là trung trực của BHc) $\Delta$DIC când)BH//ICe) AD$\perp$ICg) BC > AD + AD -...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

21 tháng 3 2023

a: Xet ΔABD vuông tại B và ΔAHD vuông tại H có

AD chung

góc BAD=góc HAD

=>ΔABD=ΔAHD

b; AB=AH

DB=DH

=>AD là trung trực của BH

c: Xet ΔDBI vuông tại B và ΔDHC vuông tại H có

DB=DH

góc BDI=góc HDC

=>ΔBDI=ΔHDC

=>DI=DC

=>ΔDIC cân tại D

d: Xét ΔAIC có AB/BI=AH/HC

nên BH//IC

e: AD vuông góc BH

BH//IC

=>AD vuông góc IC

Đúng(0)

PT

Phương Thảo

16 tháng 4 2021

cho $\Delta$ABC vuông tại A có AB>AC . Lấy M là 1 điểm tùy ý . Qua M kể đường thẳng vuông góc với BC và cắt AB tại I ,cắt AC tại Da/ CM :$\Delta ABC\sim\Delta MDC$b/ CM : BI.BA=BM.BCc/ CM : góc BAM=góc ICB từ đó CM: AB là tia phân giác góc MAK ($CI\cap BD$ tại k)d/ cho AB=8cm và AC=6 cm . Khi AM là tia phân giác trong$\Delta ABC$ hãy tính diện tích tứ giác...

Đọc tiếp

#Toán lớp 8

0

MT

Minh Tâm Nguyễn

10 tháng 5 2023

Cho $\Delta ABC$ vuông tại $A$ $\left(AB< AC\right)$ có đường cao $AH$ $a$) Chứng minh $\Delta HBA\sim$ $\Delta ABC$$b$) Trên đoạn thẳng $AH$ lấy điểm $D$. Qua $C$ vẽ đường thẳng vuông góc với $BD$ cắt tia $AH$ tại $E$. Chứng minh $\widehat{HBD}=\widehat{HEC}$ và $BH.CH=HD.HE$$c$) Chứng...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

10 tháng 5 2023

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

góc B chung

=>ΔHBA đồng dạng với ΔABC

Đúng(0)

C

Ctuu

25 tháng 4 2021

Cho $\Delta$ABC vuông tại A (AB<AC),AH là đường cao.Chứng minh:a)Chứng minh:$\Delta$ABC đồng dạng $\Delta$HBA ;$^{AB^2}$=BH.BCb)Trên tia AB lấy D sao cho B là trung điểm DA.Chứng minh:$\Delta$BDH đồng dạng $\Delta$BCDc)Kẻ AK$\perp$DH.Chứng minh:CH là phân giác của góc...

Đọc tiếp

#Toán lớp 8

0

H9

HT.Phong (9A5)

CTVHS

8 tháng 5 2023

Cho $\Delta ABC$ vuông tại A, đường cao AH, Gọi D, E theo thứ tự là hình chiếu trên AB và AC a) CM: $\Delta ABC\sim\Delta HBA$b) Cho $HB=4cm;HC=9cm$ Tính $AB,DE$c)...

Đọc tiếp

#Toán lớp 8

1

2

2611

8 tháng 5 2023

`a)` Xét `\triangle ABC` vuông tại `A` có: `\hat{B}+\hat{C}=90^o`

Xét `\triangle ABH` vuông tại `H` có: `\hat{B}+\hat{A_1}=90^o`

`=>\hat{C}=\hat{A_1}`

Xét `\triangle ABC` và `\triangle HBA` có:

`{:(\hat{C}=\hat{A_1}),(\hat{B}\text{ là góc chung}):}}=>\triangle ABC` $\backsim$ `\triangle HBA` (g-g)

`b)` Ta có: `BC=HB+HC=4+9=13(cm)`

Xét `\triangle ABC` vuông tại `A` có: `AH` là đường cao

`@AH=\sqrt{BH.HC}=6 (cm)`

`@AB=\sqrt{BH.BC}=2\sqrt{13}(cm)`

Ta có: `\hat{DEA}=\hat{ADH}=\hat{AEH}=90^o`

`=>` Tứ giác `AEHD` là hcn `=>DE=AH=6(cm)`

`c)` Xét `\triangle AHB` vuông tại `H` có: `HD \bot AB=>AH^2=AD.AB`

Xét `\triangle AHC` vuông tại `H` có: `HE \bot AC=>AH^2=AE.AC`

`=>AD.AB=AE.AC`

loading...

Đúng(3)

H9

HT.Phong (9A5)

CTVHS

8 tháng 5 2023

Cảm ơn anh nhiều

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

14 tháng 9 2023

Cho tam giác $ABC$ vuông tại $A\left( {AB < AC} \right)$. Kẻ đường cao $AH\left( {H \in BC} \right)$.a) Chứng minh rằng $\Delta ABH\backsim\Delta CBA$, suy ra $A{B^2} = BH.BC$.b) Vẽ $HE$ vuông góc với $AB$ tại $E$, vẽ $HF$ vuông góc với $AC$ tại $F$. Chứng minh rằng $AE.AB = AF.AC$.c) Chứng minh rằng $\Delta AFE\backsim\Delta ABC$.d) Qua $A$ vẽ đường thẳng song song với $BC$ cắt đường thẳng $HF$ tại $I$. Vẽ...

Đọc tiếp

#Toán lớp 8

1

KS

Kiều Sơn Tùng

14 tháng 9 2023

a) Vì $AH$ là đường cao nên $\widehat {AHB} = \widehat {AHC} = 90^\circ $

Xét tam giác $ABH$ và tam giác $CBA$ có:

$\widehat B$ (chung)

$\widehat {AHB} = \widehat {CAB} = 90^\circ $ (chứng minh trên)

Suy ra, $\Delta ABH\backsim\Delta CBA$ (g.g).

Do đó, $\frac{{AB}}{{CB}} = \frac{{BH}}{{AB}}$ (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, $A{B^2} = BH.BC$ .

b)

- Vì $HE$ vuông góc với $AB$ nên $\widehat {HEA} = \widehat {HEB} = 90^\circ $

Xét tam giác $AHE$ và tam giác $ABH$ có:

$\widehat {HAE}$ (chung)

$\widehat {HEA} = \widehat {AHB} = 90^\circ $ (chứng minh trên)

Suy ra, $\Delta AHE\backsim\Delta ABH$ (g.g).

Do đó, $\frac{{AH}}{{AB}} = \frac{{AE}}{{AH}}$ (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, $A{H^2} = AB.AE$ . (1)

- Vì $HF$ vuông góc với $AC$ nên $\widehat {HFC} = \widehat {HFA} = 90^\circ $

Xét tam giác $AHF$ và tam giác $ACH$ có:

$\widehat {HAF}$ (chung)

$\widehat {AFH} = \widehat {AHC} = 90^\circ $ (chứng minh trên)

Suy ra, $\Delta AHF\backsim\Delta ACH$ (g.g).

Do đó, $\frac{{AH}}{{AC}} = \frac{{AF}}{{AH}}$ (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, $A{H^2} = AF.AC$ . (2)

Từ (1) và (2) suy ra, $AE.AB = AF.AC$ (điều phải chứng minh)

c) Vì $AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}$.

Xét tam giác $AFE$ và tam giác $ABC$ có:

$\widehat A$ (chung)

$\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}$ (chứng minh trên)

Suy ra, $\Delta AFE\backsim\Delta ABC$ (c.g.c).

d) Vì $HF$ vuông góc với $AC$ nên $CF \bot HI$, do đó, $\widehat {CFH} = \widehat {CFI} = 90^\circ $.

Vì $IN \bot CH \Rightarrow \widehat {CBI} = \widehat {HNI} = 90^\circ $.

Xét tam giác $HFC$ và tam giác $HNI$ có:

$\widehat {CHI}$ (chung)

$\widehat {HFC} = \widehat {HNI} = 90^\circ $ (chứng minh trên)

Suy ra, $\Delta HFC\backsim\Delta HNI$ (g.g).

Suy ra, $\frac{{HF}}{{HN}} = \frac{{HC}}{{HI}}$ (hai cặp cạnh tương ứng cùng tỉ lệ)

Do đó, $\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}$.

Xét tam giác $HNF$ và tam giác $HIC$ có:

$\widehat {CHI}$ (chung)

$\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}$ (chứng minh trên)

Suy ra, $\Delta HNF\backsim\Delta HIC$ (c.g.c).

Đúng(1)

6N

6.Vũ Nguyễn Hiếu lớp 7/8

25 tháng 11 2021

Cho $\Delta ABC$ vuông tại A (AB>AC).Vẽ tia phân giác của góc C cắt AB tại D.Trên cạnh BC lấy điểm E sao cho CE=CA a)Chứng minh:$\Delta CDA=\Delta CDE$ và $DE\perp BC$b)Qua C vẽ đường thẳng vuông góc với AC.Qua A vẽ đường thẳng song song với CD,hai đường này cắt nhau tại M.Chứng minh: AM=CDc)Qua B vẽ đường thẳng vuông góc với CD tại N và cắt AC tại K.Chứng minh:AK=BEvà K;E;D thẳng hàng. (❤Mọi...

Đọc tiếp

#Toán lớp 7

0

MN

Mai Ngọc Hà

29 tháng 4 2023

Cho $\Delta ABC$ vuông tại A (AB<AC).Kẻ BD là phân giác của góc ABC (D thuộc AC) trên cạnh BC lấy điểm E sao cho AB=BE
a.chứng minh $\Delta ABD=\Delta EBD$
b.so sánh AD và DC
c.đường thẳng ED cắt AB tại F, gọi S là trung điểm của FC.Chứng minh ba điểm B, D,F thẳng hàng

#Toán lớp 7

1