[1+2/1]x[1+2/2]x[1+2/3]x...x[1+3/32]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2022
a: \(\dfrac{96}{\left(x-4\right)\left(x+4\right)}+\dfrac{7+x}{4-x}=\dfrac{2x-1}{x+4}-3\)
\(\Leftrightarrow\dfrac{96}{\left(x-4\right)\left(x+4\right)}-\dfrac{\left(x+7\right)\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{\left(2x-1\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}-\dfrac{3\left(x-4\right)\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}\)
Suy ra: \(96-x^2-11x-28=2x^2-9x+4-3\left(x^2-16\right)\)
\(\Leftrightarrow-x^2-11x+68=2x^2-9x+4-3x^2+48\)
\(\Leftrightarrow-x^2-11x+68=-x^2-9x+52\)
=>-11x+68=-9x+52
=>-2x=-16
hay x=8(nhận)
b: \(\dfrac{2}{x-1}+\dfrac{3}{x-2}=\dfrac{3}{x-3}\)
\(\Leftrightarrow2\left(x-2\right)\left(x-3\right)+3\left(x-1\right)\left(x-3\right)=3\left(x-1\right)\left(x-2\right)\)
\(\Leftrightarrow2\left(x^2-5x+6\right)+3\left(x^2-4x+3\right)=3\left(x^2-3x+2\right)\)
\(\Leftrightarrow2x^2-10x+12+3x^2-12x+9=3x^2-9x+6\)
\(\Leftrightarrow5x^2-22x+21-3x^2+9x-6=0\)
\(\Leftrightarrow2x^2-13x+15=0\)
\(\Leftrightarrow2x^2-10x-3x+15=0\)
=>(x-5)(2x-3)=0
=>x=5(nhận) hoặc x=3/2(nhận)
25 tháng 7 2023
6:=(3/2)*(3/2)^2*(3/2)^4=(3/2)^7
7: =(1/2)^7*2^3*2^5*2^8=2^9
8: =(-1/7)^4*5^4=(-5/7)^4
9: =2^2*2^5:(2^3/2^4)
=2^7/2=2^6
10: =(1/7)^3*7^2=1/7
H9
HT.Phong (9A5)
CTVHS
22 tháng 6 2023
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)
23 tháng 10 2018
\(\left(2x-1\right)^3-4x^2\left(2x-3\right)=5.\)
\(\Leftrightarrow8x^3-12x^2+6x-1-8x^3+12x^2=5\)
\(\Leftrightarrow6x-1=5\)
\(\Leftrightarrow6x=6\)
\(\Leftrightarrow x=1\)
23 tháng 10 2018
\(\left(x+4\right)^3-x^2\left(x+12\right)=15.\)
\(\Leftrightarrow x^3+12x^2+48x+64-x^3-12x^2=15\)
\(\Leftrightarrow48x+64=15\)
\(\Leftrightarrow48x=-49\)
\(\Leftrightarrow x=\frac{-49}{48}\)
H9
HT.Phong (9A5)
CTVHS
14 tháng 7 2023
\(6-2\left(x-1\right)=4\)
\(\Rightarrow2\left(x-1\right)=6-4\)
\(\Rightarrow2\left(x-1\right)=2\)
\(\Rightarrow x-1=1\)
\(\Rightarrow x=1+1=2\)
________________
\(2\cdot\left(x-2\right)+1=7\)
\(\Rightarrow2\cdot\left(x-2\right)=7-1\)
\(\Rightarrow2\cdot\left(x-2\right)=6\)
\(\Rightarrow x-2=3\)
\(\Rightarrow x=3+2=5\)
_______________
\(\left(2\cdot x-3\right)+4=9\)
\(\Rightarrow2\cdot x-3=5\)
\(\Rightarrow2\cdot x=3+5\)
\(\Rightarrow2\cdot x=8\)
\(\Rightarrow x=\dfrac{8}{2}=4\)
________________
\(\left(3\cdot x-2\right)-1=3\)
\(\Rightarrow3\cdot x-2=3+1\)
\(\Rightarrow3\cdot x-2=4\)
\(\Rightarrow3\cdot x=6\)
\(\Rightarrow x=\dfrac{6}{3}=2\)
14 tháng 7 2023
a: =>2(x-1)=2
=>x-1=1
=>x=2
b: =>2(x-2)=6
=>x-2=3
=>x=5
c; =>2x-3=5
=>2x=8
=>x=4
d: =>3x-2=4
=>3x=6
=>x=2
e: =>2(6-x)=4
=>6-x=2
=>x=4
f: =>x-2=5
=>x=7
g: =>10-2x=4
=>2x=6
=>x=3
h: =>2x+4=3
=>2x=-1
=>x=-1/2
j: =>x+2=12
=>x=10
l: =>2x+3=3
=>2x=0
=>x=0
12 tháng 7 2019
a) \(\frac{x}{x+1}=\frac{1}{2}\)
=> 2x = x + 1
=> 2x - x = 1
=> x = 1
b) \(\frac{x}{2}=\frac{x}{3}\)
=> 3x = 2x
=> 3x - 2x = 0
=> x = 0
c) \(\frac{x+1}{2}=\frac{x+1}{2017}\)
=> \(2017\left(x+1\right)=2\left(x+1\right)\)
=> 2017x + 2017 = 2x + 2
=> 2017x - 2x = 2 - 2017
=> 2015x = -2015
=> x = -2015 : 2015
=> x = -1
i) \(\frac{3}{x}=\frac{x}{2017}\)
=> x2 = 2017.3
=> x2 = 6051
=> \(\orbr{\begin{cases}x=\sqrt{6051}\\x=-\sqrt{6051}\end{cases}}\)
còn lại tự lm
12 tháng 7 2019
\(a,\frac{x}{x+1}=\frac{1}{2}\)
\(\Rightarrow x=\frac{1}{2}.\left(x+1\right)\)
\(\Rightarrow x=\frac{1}{2}x+\frac{1}{2}\)
\(\Rightarrow x-\frac{1}{2}x=\frac{1}{2}\)
\(\Rightarrow\frac{1}{2}x=\frac{1}{2}\)
\(\Rightarrow x=1\)
\(b,\frac{x}{2}=\frac{x}{3}\)
\(\Rightarrow x=\frac{x}{3}.2\)
\(\Rightarrow x=\frac{2x}{3}\)
\(\Rightarrow3x=2x\)
\(\Rightarrow x=0\)
\(c,\frac{x+1}{2}=\frac{x+1}{2017}\)
\(\Rightarrow x+1=\frac{x+1}{2017}.2\)
\(\Rightarrow x+1=\frac{2x+2}{2017}\)
\(\Rightarrow2017x+2017=2x+2\)
\(\Rightarrow2017x-2x=2-2017\)
\(\Rightarrow2015x=-2015\)
\(\Rightarrow x=-1\)
\(i,\frac{3}{x}=\frac{x}{2017}\)
\(\Rightarrow x=3:\frac{x}{2017}\)
\(\Rightarrow x=\frac{6051}{x}\)
\(\Rightarrow x^2=6051\)
\(\Rightarrow x=\sqrt{6051}\)
\(o,\frac{x}{3}=\frac{x+1}{2}\)
\(\Rightarrow x=\frac{x+1}{2}.3\)
\(\Rightarrow x=\frac{3x+3}{2}\)
\(\Rightarrow2x=3x+3\)
\(\Rightarrow-x=3\)
\(\Rightarrow x=-3\)
\(m,\frac{x+1}{2}=\frac{x+2}{3}\)
\(\Rightarrow x+1=\frac{x+2}{3}.2\)
\(\Rightarrow x+1=\frac{2x+4}{3}\)
\(\Rightarrow3x+3=2x+4\)
\(\Rightarrow x=1\)
\(p,\frac{x+1}{2}=x\)
\(\Rightarrow2x=x+1\)
\(\Rightarrow x=1\)
\(m,\frac{2}{x}=\frac{x}{8}\)
\(\Rightarrow x=2:\frac{x}{8}\)
\(\Rightarrow x=\frac{16}{x}\)
\(\Rightarrow x^2=16\)
\(\Rightarrow x=4\)
\(Q,\frac{x^2}{2}=\frac{8}{x^2}\)
\(\Rightarrow x^2=\frac{8}{x^2}.2\)
\(\Rightarrow x^2=\frac{16}{x^2}\)
\(\Rightarrow x^4=16\)
\(\Rightarrow x=2\)
\(r,\frac{x^3}{2}=\frac{32}{x}\)
\(\Rightarrow x^3=\frac{32}{x}.2\)
\(\Rightarrow x^3=\frac{64}{x}\)
\(\Rightarrow x^4=64\)
\(\Rightarrow x=\sqrt[4]{64}\)
17 tháng 9 2023
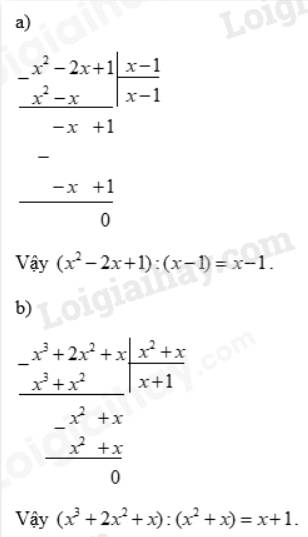
Vậy \(( - 32{x^5} + 1):( - 2x + 1) = 16{x^4} + 8{x^3} + 4{x^2} + 2x + 1\).
Thời gian có hạn copy cái này hộ mình vào google xem nha :
https://lazi.vn/quiz/d/16491/nhac-edm-la-loai-nhac-the-loai-gi
Vào xem xong các bạn nhận được 1 thẻ cào mệnh giá 100k nhận thưởng bằng cách nhắn tin vs mình và 1 phần thưởng bí mật là chiếc áo đá bóng,....
Có 300 giải nhanh nha đã có 241 người nhận rồi
OK