Cho hình vuông ABCD,M là điểm chính giữa AB.AC cắt DM tại E và diện tích của BCEM là 400cm2.Tính diện tích của ABCD.
Mong các bạn trình bày chi tiết
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
11 tháng 6 2021
Nối AN và EN
Xét các tam giác AMC và ANC đều = \(\frac{1}{4}\) diện tích hình bình hành = 15 cm2. Mặt khác 2 tam giác này có chung đáy AC \(\Rightarrow\)chiều cao hạ từ đỉnh M xuống đáy AC = chiều cao từ đỉnh N đáy AC.
Xét tam giác ENC và EMC chung đáy EC, chiều cao bằng nhau \(\Rightarrow\)\(S_{ENC}=S_{EMC}\left(1\right)\)
Xét tam giác EDN và ENC chung đỉnh E, đáy DN = NC \(\Rightarrow\)\(S_{EDN}=S_{ENC}\left(2\right)\)
Xét \(S_{AMD}\) = \(S_{AMC}\) có chung AME \(\Rightarrow\)\(S_{AED}=S_{EMC}\left(3\right)\)
Từ (1) ; (2) và (3) \(\Rightarrow\) \(S_{EMC}=S_{ENC}=S_{EDN}=S_{AED}\)
Ta có \(S_{MBC}=\) 15 cm2 \(\Rightarrow\) \(S_{ACD}\)= 15 x 2 = 30 (cm2)
Mà \(S_{ACD}\) \(=S_{ENC}+S_{EDN}+S_{AED}\) và 3 tam giác này bằng nhau nên :
\(S_{ENC}\) = 30 : 3 = 10 (cm2) mà \(S_{ENC}\) = \(S_{MEC}\)
Vậy diện tích MEC = 10 cm2.
NC
11 tháng 6 2021
\(S_{AMD}=\frac{1}{2}S_{MDC}\)vì đáy \(AM=\frac{1}{2}DC\)và chiều cao kẻ từ \(D\)đến \(AM\)bằng chiều cao kẻ từ \(M\)đến \(DC\)vì cả hai chiều cao đều là chiều cao của hình thang
\(S_{AMD}=\frac{1}{2}S_{MDC}\)mà chung đáy \(MD\)nên chiều cao \(AH=\frac{1}{2}\)chiều cao \(CK\)
Ta có: Chiều cao \(AH\)cũng chính là chiều cao \(\Delta AME\)và chiều cao \(CK\)cũng chính là chiều cao của \(\Delta MEC\)
\(S_{AME}=\frac{1}{2}S_{MEC}\)vì chung đáy \(ME\)và chiều cao \(AH=\frac{1}{2}CK\)
\(\Rightarrow\)Coi \(S_{AME}\)là một phần, \(S_{MEC}\)là hai phần, \(S_{MAC}\)là 3 phần
Ta có: \(S_{MAC}=S_{MBC}\)vì đáy \(MA=MB\)và chung chiều cao kẻ từ \(C\)đến \(AB\)
\(S_{MEC}=15:\left(1+2\right).2=10\left(cm^2\right)\)
Vậy \(S_{MEC}=10cm^2\)
14 tháng 3 2023
a: \(S_{BNDA}=\dfrac{1}{2}\cdot\left(BN+AD\right)\cdot AB=\dfrac{1}{2}\cdot20\cdot\left(10+20\right)=30\cdot10=300\left(cm^2\right)\)
b: Xét ΔMAD vuông tại A và ΔNBA vuông tại B có
MA=NB
AD=BA
=>ΔMAD=ΔNBA
=>góc AMD=góc BNA
=>góc DAN+góc ADM=90 độ
=>DM vuông góc AN
Vì AM<AD nên MO<DO
\(S_{ADN}=\dfrac{1}{2}\cdot DO\cdot AN;S_{AMN}=\dfrac{1}{2}\cdot MO\cdot AN\)
mà DO>MO
nên \(S_{ADN}>S_{AMN}\)
=>\(S_{DON}>S_{MON}\)
CM
27 tháng 8 2018
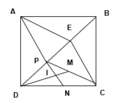
Vẽ hình đúng
a) Tính đúng diện tích hình vuông ABCD
b)-Lập luận đúng diện tích các tam giác ADP, APE, AEB, CPD, CPE, CEB bằng nhau và bằng 1 6 diện tích hình vuông ABCD.
-Lập luận được diện tích hình AECP bằng 1 3 diện tích hình vuông ABCD
-Tính đúng kết quả 12cm2
c)- Lập luận đúng diện tích tam giác DPM và DPN bằng nhau
- Lập luận đúng diện tích tam giác PMI và DNI bằng nhau
OY
7 tháng 6 2021
a) Diện tích hình vuông ABCD là:
6 x 6 = 36 ( cm2 )
b) Diện tích hình tam giác ABD là:
36 : 2 = 18 ( cm2 )
Diện tích hình tam giác APE là:
18 : 3 = 6 ( cm2 )
Diện tích hình AECP là :
6 x 2 = 12 ( cm2 )
c) Diện tích tam giác DPM = DPN= \(\dfrac{1}{2}\)diện tích tam giác DPC . Vì 2 tam giác DPM và tam giác DPC có cùng chiều cao và MP=\(\dfrac{1}{2}\) PC ; ND=\(\dfrac{1}{2}\)DC.
Diện tích tam giác DPM = diện tích tam giác DPN và đều có chung tam giác IPD nên diện tích tam giác IPM = diện tích tam giác IDN.
16 tháng 3 2020
#novectorpicture
a)
Diện tích hình vuông ABCD là:
\(6\times6=36\left(cm^2\right)\)
b)
_Ta có:
\(S_{\Delta ADP}=S_{\Delta APE}=S_{\Delta AEB}=S_{\Delta CPD}=S_{\Delta CPE}=S_{\Delta CEB}=\frac{1}{3}S_{ABCD}\)(do các tam giác có cùng chiều cao và các đáy bằng nhau: BE = EP = PD)
_Lại có:
\(S_{AECP}=\frac{1}{3}S_{ABCD}\)
\(\Rightarrow S_{AECP}\)là:
\(\frac{1}{3}\times36=12\left(cm^2\right)\)
c)
_\(S_{\Delta DPM}=S_{\Delta DPN}=\frac{1}{2}S_{\Delta DPC}\)(do \(\Delta DPM\)và \(\Delta DPC\)có cùng chiều cao và \(MP=\frac{1}{2}PC\); \(ND=\frac{1}{2}DC\))
_\(S_{\Delta DPM}=S_{\Delta DPN}\)và đều có chung \(\Delta IPD\)
\(\Rightarrow S_{\Delta PMI}=S_{\Delta DNT}\)
Đáp số:....
30 tháng 6 2017
Diện tích hình vuông ABCD là
6 x 6 = 36 ( cm )
b)-Diện tích các tam giác ADP, APE, AEB, CPD, CPE, CEB bằng nhau và bằng1/3 diện tích hình vuông ABCD. Vì các tam giác
này đều có cùng chiều cao và các đáy bằng nhau BE = EP = PD
- Diện tích hình AECP bằng 1/3diện tích hình vuông ABCD. Diện tích hình AECP là :
1/3x 36 = 12(cm )
c)- Diện tích tam giác DPM = Diện tích tam giác DPN= ½ diện tích tam giác DPC . Vì 2 tam giác DPM và tam giác DPC có cùng
chiều cao và MP=1/2 PC ; ND=1/2DC. - Diện tích tam giác DPM = diện tích tam giác DPN và đều có chung tam giác IPD nên diện
tích tam giác PMI = diện tích tam giác DNT
Chúc bạn học tốt! (^ _ ^)