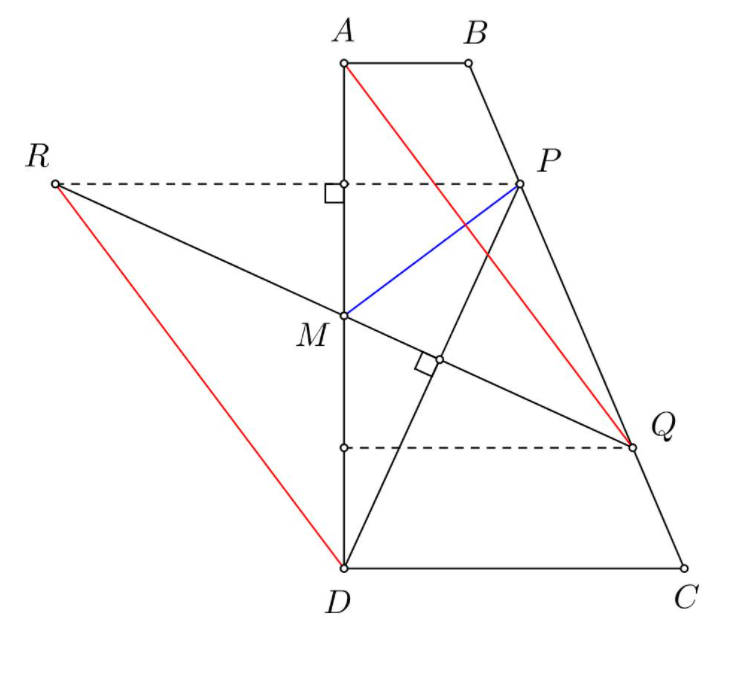
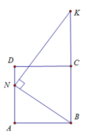
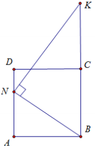
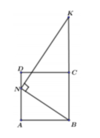
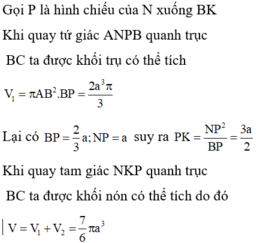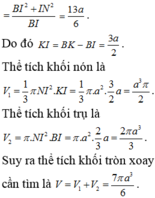Cho hình vuông ABCD. M,N thuộc BC,CD sao cho CM=2DN. P thuộc AD sao cho MP vuông góc AN, CMR DN=DP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 11 2014
câu 2
tam giác ABM bằng tam giác DBN (c.g.c) nên BM=BN và ABM=DBN ta có ABM+MBD=60 nên DBN+MBD=60 hay MBN =60 tam giác MBN đều
CM
30 tháng 9 2017
Đáp án D
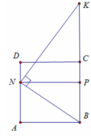
Gọi P là hình chiếu của N xuống BK
Khi quay tứ giác ANPB quanh trục BC ta được khối trụ có thể tích V 1 = πAB 2 . BP = 2 a 3 π 3
Lại có B P = 2 3 a ; N P = a suy ra P K = N P 2 B P = 3 a 2
Khi quay tam giác NKP quanh trục BC ta được khối nón có thể tích do đó V = V 1 + V 2 = 7 6 πa 3
CM
22 tháng 5 2018
Phương pháp:
Công thức tính thể tích của khối trụ có bán kính đáy R và chiều cao h: V = π R 2 h
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h: V = 1 3 π R 2 h
Cách giải:
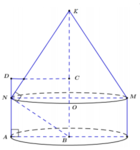
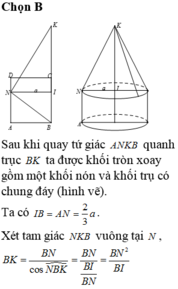
Khi quay tứ giác ANKB quanh trục BK ta được hình trụ có bán kính đáy AB, chiều cao AN và hình nón có bán kính đáy AB, chiều cao K O = B K − A N
26 tháng 2 2023
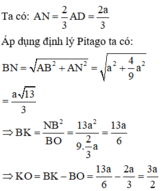
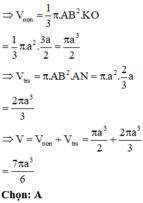
Gọi K là giao điểm của MP và NQ
Kẽ MH, QE lần lược vuông góc với DC, BC tại H,E. I, F là giao điểm của QE với MP và MH
Ta có QE //DC
=> MIQ = MPH (góc đồng vị)
MIQ = QNE ( + NQE = 90)
=> MPH = QNE (1)
Xét tam giác QNE và tam giác MPH có
Góc MPH = góc QNE
Góc MHP = góc QEN = 90
MH = QE (cùng bằng cạnh hình vuông)
=> Tam giác QNE = tam giác MPH
=> NQ = PM