 làm giúp em vs !
làm giúp em vs !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


16. B
17. A
18. A
19. A
20. C
21. A
22. B
23. C
24. D
25. C
26. D
27. A
28. D

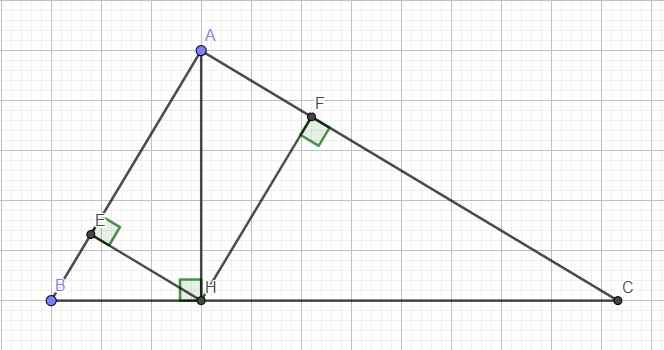
AH vuông góc BC nên các tam giác ABH và ACH là các tam giác vuông tại H
a. Áp dụng hệ thức lượng trong tam giác vuông ABH với đường cao HE:
\(AH^2=AE.AB\) (1)
Áp dụng hệ thức lượng trong tam giác vuông ACH:
\(AH^2=AF.AC\) (2)
(1);(2) \(\Rightarrow AE.AB=AF.AC\)
b. Khi \(AH^2=BH.CH\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\)
Xét hai tam giác vuông ABH và CAH có:
\(\left\{{}\begin{matrix}\dfrac{AH}{CH}=\dfrac{BH}{AH}\\\widehat{AHB}=\widehat{CHA}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta ABH\sim\Delta CAH\left(c.g.c\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{ACH}\)
Mà \(\widehat{ACH}+\widehat{HAC}=90^0\Rightarrow\widehat{BAH}+\widehat{HAC}=90^0\)
\(\Rightarrow\widehat{BAC}=90^0\Rightarrow\) tứ giác AEHF là hình chữ nhật (có 3 góc vuông)
c.
Do AEHF là hình chữ nhật \(\Rightarrow AH=EF\) (hai đường chéo bằng nhau) (3)
Mặt khác \(\widehat{BAC}\) vuông nên tam giác ABC vuông tại A
\(\Rightarrow AB.AC=AH.BC\) (4)
(3);(4) \(\Rightarrow AB.AC=EF.BC\)

a) \(\left(2x-1\right)\left(x^2-x+1\right)+x^2\left(3-2x\right)=2\)
\(\Rightarrow2x^3-2x^2+2x-x^2+x-1+3x^2-2x^3=2\)
\(\Rightarrow\left(2x^3-2x^3\right)-\left(2x^2+x^2-3x^2\right)+\left(2x+x\right)-1=2\)
\(\Rightarrow3x-1=2\)
\(\Rightarrow3x=2-1\)
\(\Rightarrow3x=1\)
\(\Rightarrow x=\dfrac{1}{3}\)

Câu 31:
#include <bits/stdc++.h>
using namespace std;
long long n,i,x,dem;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (30%x==0) dem++;
}
cout<<dem;
return 0;
}

a: Ta có: \(\left(\dfrac{3}{5}-\dfrac{7}{4}\right):\dfrac{23}{10}\)
\(=\dfrac{12-35}{20}\cdot\dfrac{10}{23}\)
\(=\dfrac{-23\cdot10}{23\cdot20}=-\dfrac{1}{2}\)
b: Ta có: \(\left(-\dfrac{2}{3}+\dfrac{3}{4}\right)^2\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{144}\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{60}-\dfrac{11}{5}=\dfrac{1}{60}-\dfrac{132}{60}=\dfrac{-131}{60}\)






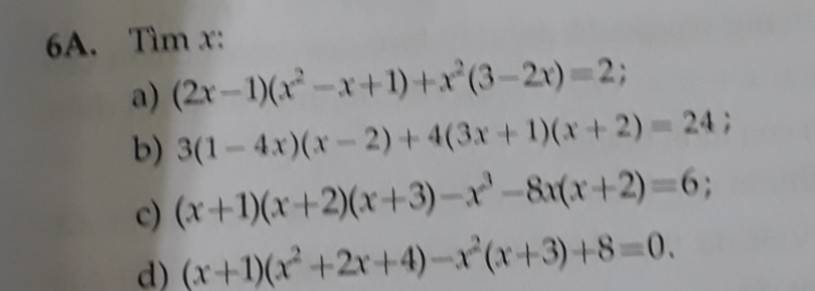 giúp em làm vs ạ
giúp em làm vs ạ
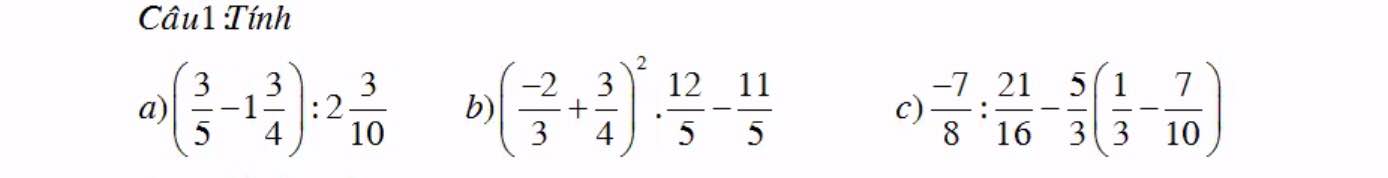

Lời giải:
\(S=\frac{1}{2^2}-\frac{1}{2^4}+\frac{1}{2^6}-......+\frac{1}{2^{2002}}-\frac{1}{2^{2004}}\)
\(2^2S=1-\frac{1}{2^2}+\frac{1}{2^4}-.....+\frac{1}{2^{2000}}-\frac{1}{2^{2002}}\)
Cộng theo vế:
\(S+4S=1-\frac{1}{2^{2004}}<1\)
$5S< 1$
$S< \frac{1}{5}$ hay $S< 0,2$
Ta có đpcm.