tìm giá trị của a để 4a2/a3+4a đạt giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 6 2017
a) M có nghĩa khi a 3 - 4 a ≠ 0 ⇔ a ≠ { 0 ; ± 2 }
b) Rút gọn thu được: M = a ( a 2 + 4 a + 4 ) a ( a 2 − 4 ) = a + 2 a − 2
c) M = − 3 ⇔ a + 2 a − 2 = − 3 ⇔ a = 1 (TMĐK)
HQ
1
4 tháng 3 2022
\(M=\dfrac{4a}{a^2+4}=\dfrac{\left(a^2+4\right)-\left(a^2-4a+4\right)}{a^2+4}=1-\dfrac{\left(a-2\right)^2}{a^2+4}\)
-Vì \(\left(a-2\right)^2\ge0;a^2+4>0\) nên \(\dfrac{\left(a-2\right)^2}{a^2+4}\ge0\)
\(\Rightarrow M=1-\dfrac{\left(a-2\right)^2}{a^2+4}\le1\)
\(M_{max}=1\Leftrightarrow\dfrac{\left(a-2\right)^2}{a^2+4}=0\Leftrightarrow\left(a-2\right)^2=0\Leftrightarrow a-2=0\Leftrightarrow a=2\).
V
1
11 tháng 7 2023
a) \(A=\dfrac{3}{x-1}\)
Điều kiện \(|x-1|\ge0\)
\(\Rightarrow A=\dfrac{3}{x-1}\ge0\)
\(GTNN\left(A\right)=0\) \(\Rightarrow x-1=+\infty\Rightarrow x\rightarrow+\infty\)
b) \(GTLN\left(A\right)\) không có \(\left(A=\dfrac{3}{x-1}\ge0\right)\)
CM
3 tháng 3 2017
Đáp án đúng : A
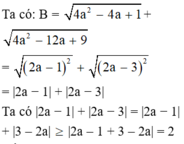
Dấu “=” xảy ra ⇔ 2 a − 1 3 − 2 a ≥ 0 ⇔ 1 2 ≤ a ≤ 3 2
Vậy GTNN của B là 2 khi 1 2 ≤ a ≤ 3 2
P
2
HP
1 tháng 7 2016
Vì |x-2| \(\ge\) 0 với mọi x
=>\(\frac{1}{2}-\left|x-2\right|\le\frac{1}{2}\) với mọi x
=>MaxA=1/2
Dấu "=" xảy ra <=> \(\left|x-2\right|=0< =>x=2\)
Vậy..............
9 tháng 11 2018
A nhỏ nhất khi \(\frac{3}{x-1}\) nhỏ nhất
=> x - 1 lớn nhất
=> x là số dương vô cùng đề sai nhá
8 tháng 7 2019
Biểu thức:
\(A=\frac{2020-x}{6-x}=\frac{2014+6-x}{6-x}=\frac{2014}{6-x}+1\)
Để A đạt giá trị lớn nhất:
thì \(\frac{2014}{6-x}\)đạt giá trị lớn nhất
<=> \(\frac{2014}{6-x}>0\) và \(6-x\)đạt giá trị bé nhất
=> \(6-x=1\Leftrightarrow x=5\)
Lúc đó A đạt giá trị lớn nhất là: \(maxA=\frac{2014}{6-5}+1=2015\)
24 tháng 3 2020
a) \(a\ne0;a\ne1\)
\(\Leftrightarrow M=\left[\frac{\left(a-1\right)^2}{3a+\left(a-1\right)^2}-\frac{1-2a^2+4a}{a^3-1}+\frac{1}{a-1}\right]:\frac{a^3+4a}{4a^2}\)
\(=\left[\frac{\left(a-1\right)^2}{a^2+a+1}-\frac{1-2a^2+4a}{\left(a-1\right)\left(a^2+a+1\right)}+\frac{1}{a-1}\right]\cdot\frac{4a^2}{a\left(a^2+4\right)}\)
\(=\frac{\left(a-1\right)^3-1+2a^2-4a+a^2+a+1}{\left(a-1\right)\left(a^2+a+1\right)}\cdot\frac{4a}{a^2+4}\)
\(=\frac{a^3-1}{a^3-1}\cdot\frac{4a}{a^2+4}=\frac{4a}{a^2+4}\)
Vậy \(M=\frac{4a}{a^2+4}\left(a\ne0;a\ne1\right)\)
b) \(M=\frac{4a}{a^2+4}\left(a\ne0;a\ne1\right)\)
M>0 khi 4a>0 => a>0
Kết hợp với ĐKXĐ
Vậy M>0 khi a>0 và a\(\ne\)1
c) \(M=\frac{4a}{a^2+4}\left(a\ne0;a\ne1\right)\)
\(M=\frac{4a}{a^2+4}=\frac{\left(a^2+4\right)-\left(a^2-4a+4\right)}{a^2+4}=1-\frac{\left(a-2\right)^2}{a^2+4}\)
Vì \(\frac{\left(a-2\right)^2}{a^2+4}\ge0\forall a\)nên \(1-\frac{\left(a-2\right)^2}{a^2+4}\le1\forall a\)
Dấu "=" <=> \(\frac{\left(a-2\right)^2}{a^2+4}=0\)\(\Leftrightarrow a=2\)
Vậy \(Max_M=1\)khi a=2