Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


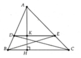
a.Ta có ΔABCΔABC cân tại A→AB=AC,ˆABC=ˆACB→ˆEBC=ˆDCBA→AB=AC,ABC^=ACB^→EBC^=DCB^
Xét ΔABD,ΔACEΔABD,ΔACE có
ˆADB=ˆAEC=90oADB^=AEC^=90o
AB=ACAB=AC
ˆBAD=ˆEACBAD^=EAC^
→ΔABD=ΔACE(c.g.c)→ΔABD=ΔACE(c.g.c)
→AE=AD→AE=AD
b.Từ câu a→AEAB=ADAC→AEAB=ADAC
→DE//BC→DE//BC
Mà ˆEBC=ˆDCBEBC^=DCB^
→BCDE→BCDE là hình thang cân

Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Do đó: ED//BC
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
mà EC=BD
nên BEDC là hình thang cân

a) Ta có :
\(AB=AC\) (Δ ABC cân tại A)
\(\Rightarrow AE+BE=AD+DC\)
mà \(AE=BE\) (CE là trung tuyến nên E là trung điểm AB)
\(AD=DC\) (BD là trung tuyến nên D là trung điểm AC)
\(\Rightarrow AE=AD\)
Xét Δ ABD và Δ ACE có :
\(AB=AC\) (Δ ABC cân tại A)
Góc A chung
\(AE=AD\left(cmt\right)\)
⇒ Δ ABD = Δ ACE (góc, cạnh, góc)
\(\Rightarrow BD=CE\)
b) Xét tứ giác BCDE có :
\(\widehat{EBC}=\widehat{DCB}\) (Δ ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}\))
\(BD=CE\left(cmt\right)\)
⇒ Tứ giác BCDE là hình thang cân
c) Ta có :
CE là trung tuyến Δ ABC
BD là trung tuyến Δ ABC
⇒ ED là đường trung bình Δ ABC
\(\Rightarrow ED=\dfrac{1}{2}BC\)
mà H là trung điểm BC (Δ ABC cân tại A nên AH vừa là đường cao và trung tuyến)
\(\Rightarrow ED=BH\)
Xét tứ giác BHDE có :
ED song song BH (BCDE là hình thang cân nên ED song song BC)
\(ED=BH\left(cmt\right)\)
⇒ Tứ giác BHDE là hình bình hành.

Tk:
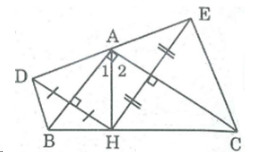
a) Điểm D đối xứng điểm H qua trục AB
⇒ AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực) ⇒ ∆ ADH cân tại A
Suy ra: AB là tia phân giác của ˆDAH⇒ˆDAB=ˆA1DAH^⇒DAB^=A^1
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A
Suy ra: AC là đường phân giác của ˆHAE⇒ˆA2=ˆEACHAE^⇒A^2=EAC^
Ta có: ˆDAE=ˆDAH+ˆHAEDAE^=DAH^+HAE^=2(ˆA1+ˆA2)=2.900=1800=2(A^1+A^2)=2.900=1800
Suy ra D, A, E thẳng hàng
Lại có: AD = AE (vì cùng bằng AH)
Nên điểm A là trung điểm của đoạn DE
Vậy điểm D đối xứng với điểm E qua điểm A.
b) Tam giác DHE có HA là trung tuyến và AH=AD=AE=12DEAH=AD=AE=12DE nên tam giác DHE vuông tại H.
c) Xét ΔADBΔADB và ΔAHBΔAHB có:
+) AB chung
+) BD = BH ( vì AB là trung trực của DH)
+) AD = AH (vì AB là trung trực của DH)
⇒ΔADB=ΔAHB(c.c.c)⇒ΔADB=ΔAHB(c.c.c)
⇒ˆAHB=ˆADB=900⇒AHB^=ADB^=900 (hai góc tương ứng)
⇒BD⊥DE⇒BD⊥DE
Xét ΔAECΔAEC và ΔAHCΔAHC có:
+) AC chung
+) EC = HC ( vì AC là trung trực của EH)
+) AE = AH (vì AC là trung trực của EH)
⇒ΔAEC=ΔAHC(c.c.c)⇒ΔAEC=ΔAHC(c.c.c)
⇒ˆAHC=ˆAEC=900⇒AHC^=AEC^=900 (hai góc tương ứng)
⇒EC⊥DE⇒EC⊥DE
Suy ra BD//CE (vì cùng vuông góc với DE)
Do đó tứ giác BDEC là hình thang có 2 góc vuông kề cạnh bên DE nên BDEC là hình thang vuông.
d) Do AB là đường trung trực của DH nên BD=BH (5)
Do AC là đường trung trực của EH nên CE=CH (6)
Cộng vế với vế của (5) và (6) ta có BD+CE=BH+CHBD+CE=BH+CH hay BD+CE=BC

a: Xét ΔAEC vuông tại E và ΔADB vuông tại D có
AB=AC
góc A chung
Do đó: ΔAEC=ΔADB
b: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà góc EBC=góc DCB
nên BEDC là hình thang cân
giup em voi
Hình Thang cân
Ta có: tam giác ABC là tam giác cân tại A.
=> góc B= góc C
Vì BD và CE là phân giác góc B và C
=> góc DBC = góc EBD = góc DCE = góc ECB
Xét tam giác EBC và tam giác DBC có:
góc ECB = góc DBC
góc BCD = góc EBC
Chung cạnh BC