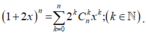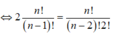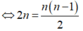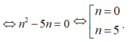Cho đa thức P(x)=anxn+an-1xn-1+....+a1x+a0 (các hệ số là số nguyên).Chứng minh rằng nếu P(x) có một nghiệm x=x0 nhận giá trị nguyên (khác 0) thì x0 là ước của a0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gỉa sử P(x) có một nghiệm nguyên là \(x_0\left(x_0\ne0\right)\)
Ta có \(P\left(x\right)=a_nx_0^n+a_{n-1}x_0^{n-1}+...+a_1x_0+a_0=0.\)
Như vậy \(P\left(x_0\right)=0⋮x_0\)và các số hạng \(a_nx_0^n+a_{n-1}x_0^{n-1}+...+a_1x_0\)đều chia hết cho \(x_0\), suy ra \(a_0\)cũng phải chia hết \(x_0\)tức \(x_0\)là ước của \(a_0\)

Ta có
1 C n 2 + 7 C n 3 = 1 n ⇔ n ≥ 3 2 n n - 1 + 7 . 3 ! n n - 1 n - 2 = 1 n ⇔ n ≥ 3 n 2 - 5 n - 36 = 0 ⇔ n = 9
Suy ra a 8 là hệ số của x 8 trong khai triển 8 1 - x 8 + 9 1 - x 9
Vậy ta thu được a 8 = 8 . C 8 8 + 9 . C 9 8 = 89
Đáp án C

Chọn D
Đạo hàm hai vế f(x)
![]()
![]()
![]()
Số hạng tổng quát thứ k + 1 trong khai triển thành đa thức của ![]()
![]()