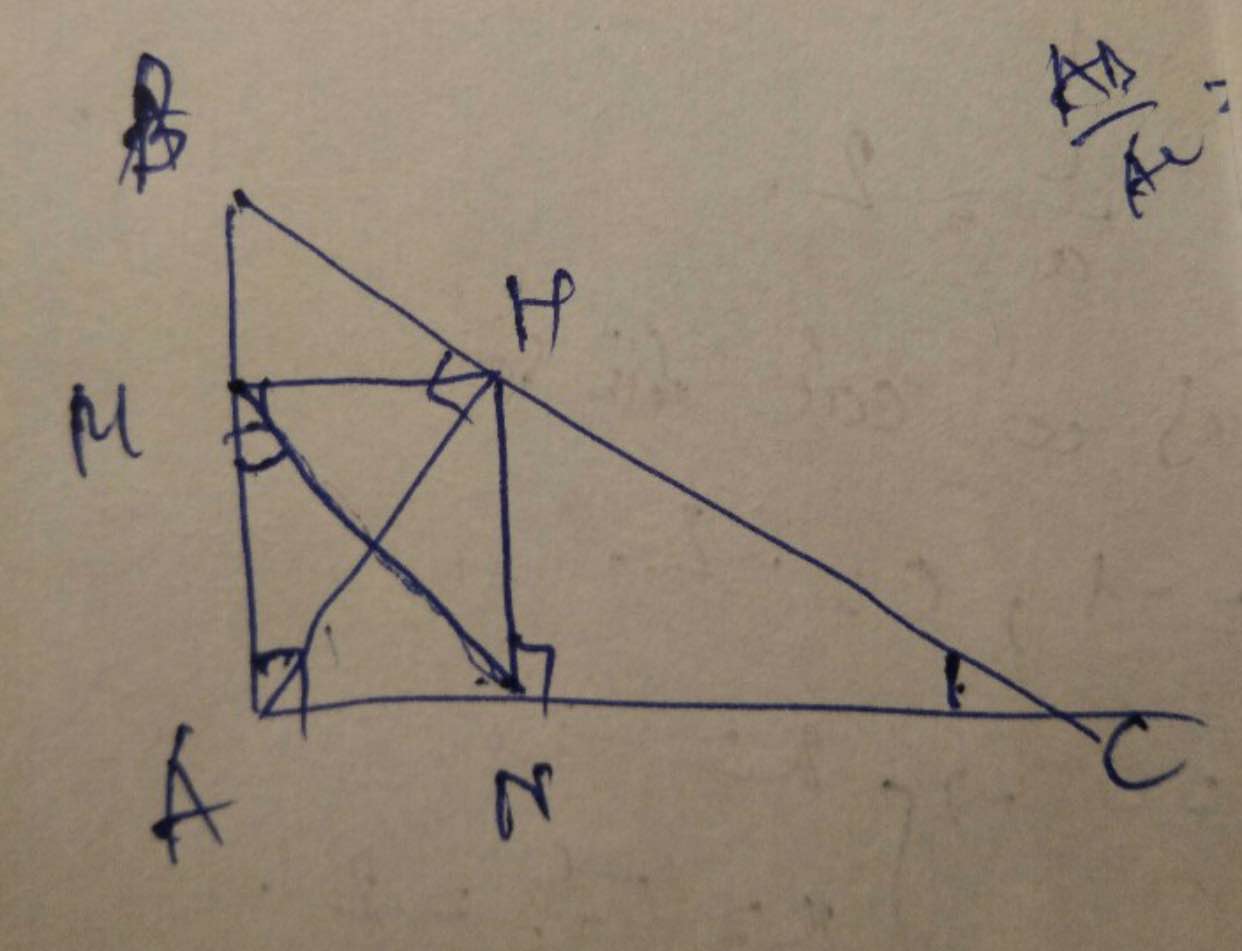
cho tam giác ABC vuông tại A,đường cao AH.gọi D,E lần lượt là hình chiếu của H lên AB và AC.chứng minh: a) \(\dfrac{AB^2}{AC^2}=\dfrac{HB}{HC}\) b) \(\dfrac{AB^3}{AC^3}=\dfrac{BD}{CE}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
18 tháng 7 2021
a) Ta có: \(\left(\dfrac{AB}{AC}\right)^2=\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}=\dfrac{BH}{HC}\)
b) Ta có: \(\left(\dfrac{CA}{AB}\right)^4=\left(\dfrac{CA^2}{AB^2}\right)^2=\left(\dfrac{CH.BC}{BH.BC}\right)^2=\dfrac{CH^2}{BH^2}=\dfrac{CE.CA}{BD.BA}\)
\(=\dfrac{CE}{BD}.\dfrac{CA}{BA}\Rightarrow\left(\dfrac{CA}{AB}\right)^3=\dfrac{CE}{BD}\)
c) Ta có: \(AH^4=\left(AH^2\right)^2=\left(BH.CH\right)^2=BH^2.CH^2\)
\(=BD.BA.CE.CA=BD.CE\left(AB.AC\right)=BD.CE.AH.BC\)
\(\Rightarrow BD.CE.BC=AH^3\)
d) Vì \(\angle HDA=\angle HEA=\angle DAE=90\Rightarrow ADHE\) là hình chữ nhật
\(\Rightarrow AH=DE\Rightarrow AH^2=DE^2=DH^2+HE^2\)
Ta có: \(3AH^2+BD^2+CE^2=2AH^2+\left(DH^2+BD\right)^2+\left(HE^2+CE^2\right)\)
\(=2.HB.HC+BH^2+CH^2=\left(BH+CH\right)^2=BC^2\)
20 tháng 7 2021
Ta có : \(AB^2=BH.BC\)
\(AC^2=CH.BC\)
Chia vế với vế ta được :
\(\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)
11 tháng 10 2023
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
ΔHDB vuông tại D có DK là trung tuyến
nên KH=KB=KD
ΔHEC vuông tại E có EI là trung tuyến
nên EI=IH=IC
\(\widehat{IED}=\widehat{IEH}+\widehat{DEH}\)
\(=\widehat{IHE}+\widehat{DAH}\)
\(=\widehat{HAB}+\widehat{HBA}=90^0\)
=>IE vuông góc ED(1)
\(\widehat{KDE}=\widehat{KDH}+\widehat{EDH}\)
\(=\widehat{KHD}+\widehat{EAH}=\widehat{HAC}+\widehat{HCA}=90^0\)
=>KD vuông góc DE(2)
Từ (1), (2) suy ra DKIE là hình thang vuông
\(S_{DKIE}=\dfrac{1}{2}\left(DK+EI\right)\cdot ED\)
\(=\dfrac{1}{2}\cdot AH\cdot\left(\dfrac{1}{2}HC+\dfrac{1}{2}HB\right)\)
\(=\dfrac{1}{4}\cdot AH\cdot BC\)
=>\(\dfrac{S_{DKIE}}{S_{ABC}}=\dfrac{1}{4}:\dfrac{1}{2}=\dfrac{1}{2}\)
10 tháng 8 2021
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(BE\cdot BA=BH^2\)
hay \(BE=\dfrac{BH^2}{BA}\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền CA, ta được:
\(CF\cdot CA=CH^2\)
hay \(CF=\dfrac{CH^2}{CA}\)
Ta có: \(\dfrac{BE}{CF}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{CA}\)
\(=\dfrac{BH^2}{CH^2}\cdot\dfrac{AC}{AB}\)
\(=\dfrac{AB^4\cdot AC}{AC^4\cdot AC}=\dfrac{AB^3}{AC^3}\)
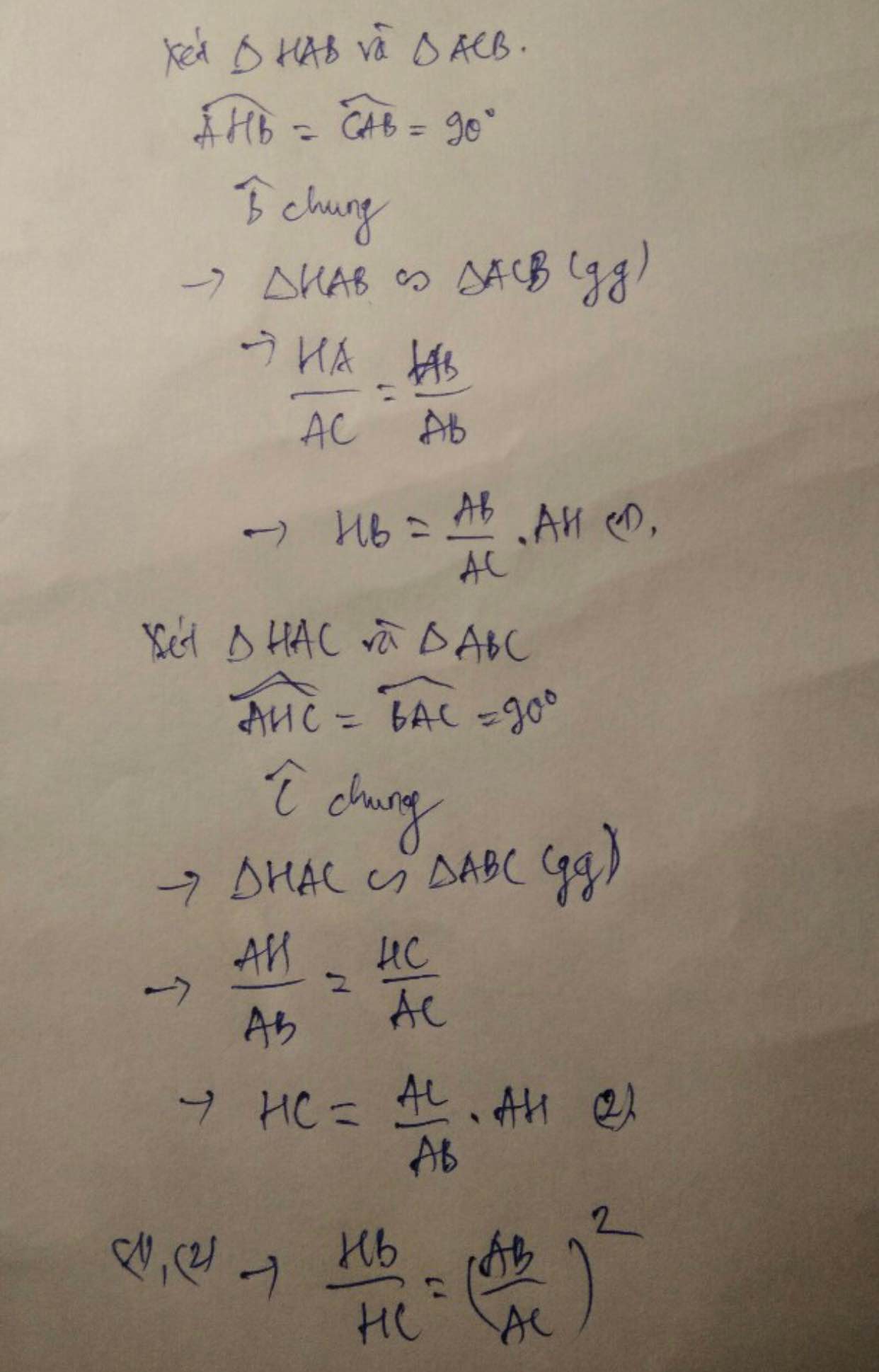
ai làm đc mk sẽ lấy nhiều nik để cho nhiều like nha