\(\sqrt{9-4\sqrt{5}}-\sqrt{9+4\sqrt{5}}\)
???
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
26 tháng 6 2023
\(c,\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}\\ =\sqrt{\sqrt{3^2}+2\sqrt{3}.1+1}+\sqrt{\sqrt{3^2}-2\sqrt{3}.1+1}\\ =\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\\ =\left|\sqrt{3}+1\right|+\left|\sqrt{3}-1\right|\\ =\sqrt{3}+1+\sqrt{3}-1\\ =2\sqrt{3}\)
\(d,\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\\ =\sqrt{\sqrt{5^2}+2.2\sqrt{5}+2^2}-\sqrt{\sqrt{5^2}-2.2\sqrt{5} +2^2}\\ =\sqrt{\left(\sqrt{5}+2\right)^2}+\sqrt{\left(\sqrt{5}-2\right)^2}\\ =\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\\ =\sqrt{5}+2-\sqrt{5}+2\\ =4\)
AH
Akai Haruma
Giáo viên
26 tháng 6 2021
\(A=\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}=\sqrt{3+1+2\sqrt{3.1}}-\sqrt{3+1-2\sqrt{3.1}}\)
\(=\sqrt{(\sqrt{3}+1)^2}-\sqrt{(\sqrt{3}-1)^2}=|\sqrt{3}+1|-|\sqrt{3}-1|=2\)
\(B=\sqrt{4+5-2\sqrt{4.5}}+\sqrt{4+5+2\sqrt{4.5}}=\sqrt{(\sqrt{4}-\sqrt{5})^2}+\sqrt{(\sqrt{4}+\sqrt{5})^2}\)
\(=|\sqrt{4}-\sqrt{5}|+|\sqrt{4}+\sqrt{5}|=2\sqrt{5}\)
AH
Akai Haruma
Giáo viên
26 tháng 6 2021
\(C\sqrt{2}=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}=\sqrt{7+1-2\sqrt{7.1}}-\sqrt{7+1+2\sqrt{7.1}}\)
\(=\sqrt{(\sqrt{7}-1)^2}-\sqrt{(\sqrt{7}+1)^2}\)
\(=|\sqrt{7}-1|-|\sqrt{7}+1|=-2\Rightarrow C=-\sqrt{2}\)
----------------------------
\(7+4\sqrt{3}=(2+\sqrt{3})^2\Rightarrow 10\sqrt{7+4\sqrt{3}}=10(2+\sqrt{3})\)
\(\Rightarrow \sqrt{48-10\sqrt{7+4\sqrt{3}}}=\sqrt{28-10\sqrt{3}}=\sqrt{(5-\sqrt{3})^2}=5-\sqrt{3}\)
\(\Rightarrow 3+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}=3+5(5-\sqrt{3})=28-5\sqrt{3}\)
\(\Rightarrow D=\sqrt{5\sqrt{28-5\sqrt{3}}}\)
18 tháng 6 2021
`a)\sqrt{9-4sqrt5}-sqrt5`
`=sqrt{5-2.2sqrt5+4}-sqrt5`
`=sqrt{(sqrt5-2)^2}-sqrt5`
`=|\sqrt5-2|-sqrt5`
`=sqrt5-2-sqrt5=-2`
`b)\sqrt{7-4sqrt3}+sqrt{4-2sqrt3}`
`=\sqrt{4-2.2sqrt3+3}+\sqrt{3-2sqrt3+1}`
`=sqrt{(2-sqrt3)^2}+sqrt{(sqrt3-1)^2}`
`=|2-sqrt3|+|sqrt3-1|`
`=2-sqrt3+sqrt3-1=1`
`c)(x-49)/(sqrtx-7)(x>=0,x ne 49)`
`=((sqrtx-7)(sqrtx+7))/(sqrtx-7)`
`=sqrtx+7`
`d)\sqrt{4+2\sqrt3}-\sqrt{13+4sqrt3}`
`=\sqrt{3+2sqrt3+1}-\sqrt{12+2.2sqrt3+1}`
`=sqrt{(sqrt3+1)^2}-\sqrt{(2sqrt3+1)^2}`
`=sqrt3+1-2sqrt3-1=-sqrt3`
`e)2+sqrt{17-4sqrt{9+4sqrt{45}}}`(câu này hơi sai)
25 tháng 6 2021
a) Ta có: \(9+4\sqrt{5}\)
\(=5+2\cdot\sqrt{5}\cdot2+4\)
\(=\left(\sqrt{5}+2\right)^2\)(đpcm)
b) Ta có: \(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}\)
=-2(ddpcm)
c) Ta có: \(\left(4-\sqrt{7}\right)^2\)
\(=16-2\cdot4\cdot\sqrt{7}+7\)
\(=23-8\sqrt{7}\)(đpcm)
d) Ta có: \(\sqrt{17-12\sqrt{2}}+2\sqrt{2}\)
\(=\sqrt{9-2\cdot3\cdot2\sqrt{2}+8}+2\sqrt{2}\)
\(=\sqrt{\left(3-2\sqrt{2}\right)^2}+2\sqrt{2}\)
\(=3-2\sqrt{2}+2\sqrt{2}=3\)(đpcm)
KH
25 tháng 6 2021
\(a.VT=4+4\sqrt{5}+5=2^2+4\sqrt{5}+\sqrt{5}^2=\left(2+\sqrt{5}\right)^2=VP\)
\(b.\) Dựa vào câu a ta có: \(9-4\sqrt{5}=\left(\sqrt{5}-2\right)^2\)
\(VT=\left|\sqrt{5}-2\right|-\sqrt{5}=\sqrt{5}-2-\sqrt{5}=-2=VP\)
\(c.VT=16-8\sqrt{7}+7=4^2-8\sqrt{7}+\sqrt{7}^2=\left(4-\sqrt{7}\right)^2=VP\)
\(d.\)
Ta có: \(17-12\sqrt{2}=8-12\sqrt{2}+9=\left(2\sqrt{2}\right)^2-12\sqrt{2}+3^2=\left(2\sqrt{2}-3\right)^2\)
\(VT=\left|2\sqrt{2}-3\right|+2\sqrt{2}=3-2\sqrt{2}+2\sqrt{2}=3=VP\)
AH
Akai Haruma
Giáo viên
20 tháng 7 2020
7.
\(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}}=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{4+3+2\sqrt{4.3}}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{(\sqrt{4}+\sqrt{3})^2}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10(2+\sqrt{3})}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{25+3-2.5\sqrt{3}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{(5-\sqrt{3})^2}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5(5-\sqrt{3})}}=\sqrt{4+\sqrt{25}}=\sqrt{4+5}=3\)
AH
Akai Haruma
Giáo viên
20 tháng 7 2020
5.
\(\sqrt{6+2\sqrt{5}-\sqrt{29+12\sqrt{5}}}=\sqrt{6+2\sqrt{5}-\sqrt{20+9+2\sqrt{20.9}}}\)
\(=\sqrt{6+2\sqrt{5}-\sqrt{(\sqrt{20}+3)^2}}=\sqrt{6+2\sqrt{5}-(\sqrt{20}+3)}=\sqrt{3}\)
6.
\(\sqrt{8+\sqrt{8}+\sqrt{20}+\sqrt{40}}-\sqrt{\sqrt{49}+\sqrt{40}}\)
\(=\sqrt{8+2\sqrt{2}+2\sqrt{5}+2\sqrt{10}}-\sqrt{7+2\sqrt{10}}\)
\(=\sqrt{(2+5+2\sqrt{2.5})+2(\sqrt{2}+\sqrt{5})+1}-\sqrt{2+5+2\sqrt{2.5}}\)
\(=\sqrt{(\sqrt{2}+\sqrt{5})^2+2(\sqrt{2}+\sqrt{5})+1}-\sqrt{(\sqrt{2}+\sqrt{5})^2}\)
\(=\sqrt{(\sqrt{2}+\sqrt{5}+1)^2}-\sqrt{(\sqrt{2}+\sqrt{5})^2}=|\sqrt{2}+\sqrt{5}+1|-|\sqrt{2}+\sqrt{5}|=1\)
H9
HT.Phong (9A5)
CTVHS
17 tháng 7 2023
1) \(\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{2^2+2\cdot2\cdot\sqrt{5}+\left(\sqrt{5}\right)^2}-\sqrt{2^2-2\cdot2\cdot\sqrt{5}+\left(\sqrt{5}\right)^2}\)
\(=\sqrt{\left(2+\sqrt{5}\right)^2}-\sqrt{\left(2-\sqrt{5}\right)^2}\)
\(=\left|2+\sqrt{5}\right|-\left|2-\sqrt{5}\right|\)
\(=2+\sqrt{5}+2-\sqrt{5}\)
\(=4\)
2) \(\sqrt{12-6\sqrt{3}}+\sqrt{12+6\sqrt{3}}\)
\(=\sqrt{3^2-2\cdot3\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}+\sqrt{3^2+2\cdot3\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{\left(3-\sqrt{3}\right)^2}+\sqrt{\left(3+\sqrt{3}\right)^2}\)
\(=\left|3-\sqrt{3}\right|+\left|3+\sqrt{3}\right|\)
\(=3-\sqrt{3}+3+\sqrt{3}\)
\(=6\)
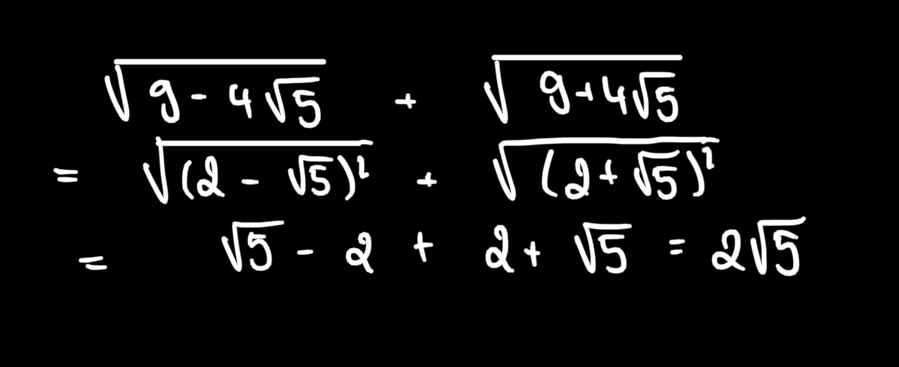
\(\sqrt{9-4\sqrt{5}}-\sqrt{9+4\sqrt{5}}\)
\(=\sqrt{5}-2-\sqrt{5}-2\)
=-4
Tại sao ra \(\sqrt{5}-2-\sqrt{5}-2\) vậy ?