Hai vật m1 và m2 được nối với nhau bằng một sợi chỉ và chúng được treo bởi một lò xo có độ cứng k (lò xo nối với m1). Khi hai vật đang ở vị trí cân bằng người ta đốt đứt sợi chỉ sao cho vật m2 rơi xuống thì vật m1 sẽ dao động điều hòa với biên độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
27 tháng 7 2019
Đáp án D
Tại vị trí lò xo thấp nhất ứng với vị trí biên ta tính được biên độ dao động của hệ :
Tại vị trí vật 2 tách khỏi hệ là vị trí biên v = 0 , A = 4cm , khi mất đi vật m 2 ta sẽ có VTCB mới
VT
11 tháng 2 2019
Đáp án D
Khi treo vật m1 thì lò xo giãn đến vị trí O2
Khi treo vật m2 thì lò xo giãn đến vị trí O1
Gọi O2 cao hơn O1 1 đoạn là b
Khi vật ở vị trí thấp nhất => có vận tốc là 0
rồi truyền cho vật vận tốc v0 dọc theo trục lò xo hướng xuống để sau đó m2
VT
27 tháng 10 2019
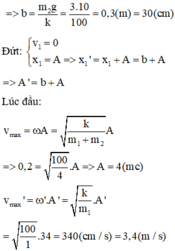
Giải thích: Đáp án A
Phương pháp: Sử dụng hệ thức độc lập theo thời gian của x và v
Cách giải:
Tại VTCB của m2 lò xo giãn một đoạn 
Tại vị trí lò xo giãn 17,07cm vật m2 có li độ 
nhận được tốc độ v0 =>
Sau đó m2 sẽ dao động điều hòa với biên độ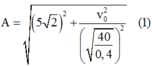 
Để sau khi cắt dây khoảng cách m1 và m2 không thay đổi thì thời điểm cắt thích hợp phải là lúc lò xo không biến dạng đồng thời vận tốc của m2 phải bằng 0.
Muốn vậy thời điểm cắt là thời điểm mà vật m2 ở biên trên (v=0) và vị trí đó chính là vị trí lò xo không biến dạng 
Từ (1) và (2) ta có: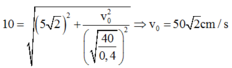 
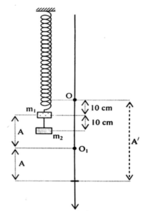
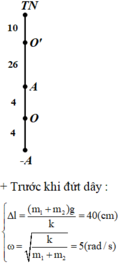
VT
7 tháng 3 2017
+ Lúc đầu chỉ có m 1 , tại VTCB O lò xo dãn 10 cm nên
+ Đưa vật đến vị trí lò xo dãn 20 cm thì vật ở dưới VTCB O đoạn x 0 = 10 c m
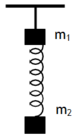
+ Lúc này gắn thêm m 2 = 3 m 1 thì VTCB của hệ bị dịch xuống đoạn:
+ Vậy, lúc này hệ ở trên VTCB O 1 đoạn 20 cm.
+ Do thả nhẹ nên hệ sẽ dao động với biên độ
A = 20 c m quanh vị trí cân bằng O 1
+ Nhưng khi đến vị trí thấp nhất thì dây đứt, nên vị trí cân bằng dịch về O.
+ Lúc này m 1 cách O đoạn 50 cm và có vận tốc bằng không nên nó sẽ dao động điều hòa quanh O với biên độ A ' = 50 c m
+ Khi m 1 lên cao nhất thì đã đi được quãng đường s 1 = 2 A ' = 100 c m (kể từ vị trí đứt dây) và mất thời gian:
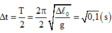
+ Trong thời gian ∆ t này vật m 2 rơi tự do nên quãng đường m 2 đi được là:
Vì dây dài b = 10 c m nên khoảng cách giữa hai vật lúc này là:
=> Chọn C.
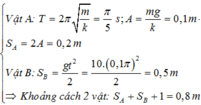
Biên độ: \(A= \Delta \ell = \dfrac{m_2.g}{k}\)
\(\Delta l\circledast\Delta m\)