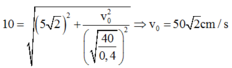Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
rồi truyền cho vật vận tốc v0 dọc theo trục lò xo hướng xuống để sau đó m2
Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm
Đáp án A
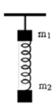
+Độ biến dạng của lò xo tại vị trí cân bằng vật m 2
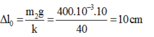
+Để vật m 2 có thể dao động điều hòa được thì lò xo phải luôn ở trạng thái bị giãn hoặc không biến dạng, hay
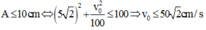
+Ta để ý rằng nếu vận tốc ban đầu 
thì khi vật đi lên vị trí cao nhất (lò xo không biến dạng), vị trí này lại trùng với biên độ của dao động nên vận tốc của vật bằng không. Ta tiến hành cắt dây hai vật sẽ cùng rơi tự do nên khoảng cách giữa chúng sẽ không thay đổi
Điều này sẽ không xảy ra với các trường hợp 
vì khi đó lò xo luôn bị biến dạng.
Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)
Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)
\(\Delta l=\frac{g}{\omega^2}=0,25m\)
\(t=0\Rightarrow x=5\sqrt{3}cm\Rightarrow l=l_0+\Delta l+x=158,66cm\)
Vậy không phương án đúng
Khi qua VTCB, tốc độ của con lắc đạt cực đại là:
\(v_{max}=\omega A =\sqrt{\dfrac{k}{m}}.A\)
\(\Rightarrow m = \dfrac{kA^2}{v_{max}^2}=\dfrac{a}{v_{max}^2}\) (vì \(kA^2=const\))
Theo đề bài ta có: \(m_3=9m_1+4m_2\)
\(\Rightarrow \dfrac{a}{v_3^2}=\dfrac{9a}{v_1^2}+\dfrac{4a}{v_2^2}\)
\(\Rightarrow \dfrac{1}{v_3^2}=\dfrac{9}{v_1^2}+\dfrac{4}{v_2^2}\)
\(\Rightarrow \dfrac{1}{v_3^2}=\dfrac{9}{20^2}+\dfrac{4}{10^2}\)
\(\Rightarrow v_3=4m/s\)
Chọn đáp án B.
Giải thích: Đáp án A
Phương pháp: Sử dụng hệ thức độc lập theo thời gian của x và v
Cách giải:
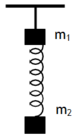
Tại VTCB của m2 lò xo giãn một đoạn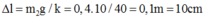
Tại vị trí lò xo giãn 17,07cm vật m2 có li độ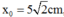
nhận được tốc độ v0 =>
Sau đó m2 sẽ dao động điều hòa với biên độ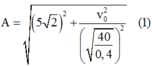
Để sau khi cắt dây khoảng cách m1 và m2 không thay đổi thì thời điểm cắt thích hợp phải là lúc lò xo không biến dạng đồng thời vận tốc của m2 phải bằng 0.
Muốn vậy thời điểm cắt là thời điểm mà vật m2 ở biên trên (v=0) và vị trí đó chính là vị trí lò xo không biến dạng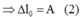
Từ (1) và (2) ta có: