Tìm giá trị của m để phương trình sau vô nghiệm: \(m^2x+2x=5+3mx\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài làm
m2x - 4x = 5 - 3mx
<=> m2x - 4x + 3mx = 5
<=> x( m2 - 4 + 3m ) = 5
Để phương trình m2x - 4x = 5 - 3mx vô nghiệm thì:
m2 - 4 + 3m = 0
<=> m2 - 3 - 1 + 3m = 0
<=> ( m2 - 1 ) - 3( 1 - m ) = 0
<=> ( m - 1 )( m + 1 ) - 3( 1 - m ) = 0
<=> ( 1 - m )( -m - 1 ) - 3( 1 - m ) = 0
<=> ( 1 - m )( -m - 1 - 3 ) = 0
<=> ( 1 - m )( -m - 4 ) = 0
<=> \(\orbr{\begin{cases}1-m=0\\-m-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}m=1\\-m=4\end{cases}\Leftrightarrow\orbr{\begin{cases}m=1\\m=-4\end{cases}}}}\)
Vậy để thương trình trên vô nghiệm thì m = 1 hoặc m = -4
# Học tốt #

3/(x^2-13x+40)+2/(x^2-8x+15)+1/(x^2-5x+6)+6/5+0
3/(x-8)(x-5)+2/(x-5)(x-3)+1/(x-3)(x-2)+6/5=0
1/(x-8)-1/(x-5)+1/(x-5)-1/(x-3)+1/(x-3)-1/(x-2)+6/5=0
1/(x-8)-1/(x-2)+6/5=0
ban tu giai tiep nhan
m^2x+2x=5-3mx
m^2x+3mx+2x=5
x(m^2+3m+2)=5
khi 0x=5 thi pt vo nghiem
m^2+3m+2=0
(m+1)(m+2)=0
m=-1 hoac m=-2

m lũy thừa 2x hả bạn? cái dạng này tớ biết sơ sơ nà, cơ mà bạn ghi đề khó hiểu quá
ta có m2x + 2x = 5 + 3m
<=> m2x + 2x - 3m = 5
<=> (m2 + 2 -3m)x = 5
<=> (m2 - m + 2m + 2)x = 5
<=> (m-1)(m+2)x = 5
* Nếu m khác 1 và m khác -2 thì x = \(\frac{5}{\left(m-1\right)\left(m+2\right)}\)
* Nếu m = 1 thì 0x = 5 => Phương trình vô nghiệm
* Nếu m = -2 thì 0x = 5 => phương trình vô nghiệm
Vậy m = {-2;1} thì phương trình vô nghiệm

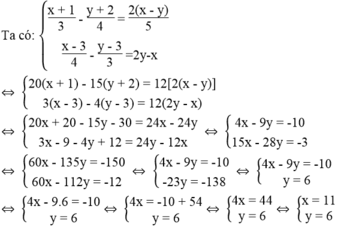
Vì (x; y) = (11; 6) là nghiệm của phương trình 3mx – 5y = 2m +1 nên ta có:
3m.11 – 5.6 = 2m + 1
⇔ 33m – 30 = 2m + 1 ⇔ 31m = 31 ⇔ m = 1
Vậy với m = 1 thì nghiệm của x + 1 3 - y + 2 4 = 2 x - y 5 x - 3 4 - y - 3 3 = 2 y - x cũng là nghiệm của phương trình 3mx – 5y = 2m + 1.

Xét hệ phương trình: m x − ( m + 1 ) y = 3 m x − 2 m y − m + 2
Ta có: D = m − ( m + 1 ) 1 − 2 m = − 2 m 2 + m + 1 = 2 m + 1 1 − m
D x = 3 m − ( m + 1 ) m + 2 − 2 m = − 6 m 2 + ( m + 2 ) ( m + 1 ) = − 5 m 2 + 3 m + 2 = 5 m + 2 1 − m
D y = m 3 m 1 m + 2 = m 2 + 2 m − 3 m = m 2 − m = m ( m − 1 )
Hệ phương trình có nghiệm duy nhất
⇔ D ≠ 0 ⇔ 2 m + 1 1 − m ≠ 0 ⇔ m ≠ − 1 2 m ≠ 1
Khi đó: x = D x D = 5 m + 2 1 − m 2 m + 1 1 − m = 5 m + 2 2 m + 1 y = D y D = m 1 − m 2 m + 1 1 − m = − m 2 m + 1
Thay giá trị của x, y vào phương trình: x + 2 y = 4 ta được:
5 m + 2 2 m + 1 − 2 m 2 m + 1 = 4 ⇔ 3 m + 2 2 m + 1 = 4 ⇔ 3 m + 2 = 8 m + 4
⇔ m = − 2 5
Đáp án cần chọn là: D

TH1: m=-1/2
BPT sẽ là -2x-3/2-3>0
=>-2x>9/2
=>x<-9/4
=>Loại
TH2: m<>-1/2
Δ=(-2)^2-4(2m+1)(3m-3)
=4-4(6m^2-6m+3m-3)
=4-4(6m^2-3m-3)
=4-24m^2+12m+12
=-24m^2+12m+16
Để BPT vô nghiệm thì -24m^2+12m+16<=0 và 2m+1<0
=>m<-1/2 và \(\left[{}\begin{matrix}m< =\dfrac{3-\sqrt{105}}{2}\\m>=\dfrac{3+\sqrt{105}}{2}\end{matrix}\right.\)
=>\(m< =\dfrac{3-\sqrt{105}}{2}\)

\(VT=\left|x-1\right|+\left|2-x\right|\ge\left|x-1+2-x\right|=1\)
\(VP=-4x^2+12x-9-1=-\left(2x-3\right)^2-1\le-1\)
\(\Rightarrow VT>VP\) ; \(\forall x\)
\(\Rightarrow\) Pt đã cho luôn luôn vô nghiệm
b.
\(\Leftrightarrow\left(m^2+3m\right)x=-m^2+4m+21\)
\(\Leftrightarrow m\left(m+3\right)x=\left(7-m\right)\left(m+3\right)\)
Để pt có nghiệm duy nhất \(\Rightarrow m\left(m+3\right)\ne0\Rightarrow m\ne\left\{0;-3\right\}\)
Khi đó ta có: \(x=\dfrac{\left(7-m\right)\left(m+3\right)}{m\left(m+3\right)}=\dfrac{7-m}{m}\)
Để nghiệm pt dương
\(\Leftrightarrow\dfrac{7-m}{m}>0\Leftrightarrow0< m< 7\)

\(\Leftrightarrow\left(m^2+2m+1\right)x-\left(7m-5\right)x=m-1\)
\(\Leftrightarrow\left(m^2-5m+6\right)x=m-1\)
Pt vô nghiệm khi: \(\left\{{}\begin{matrix}m^2-5m+6=0\\m-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=2\\m=3\end{matrix}\right.\)
Lời giải:
Ta có: \(m^2x+2x=5+3mx\)
\(\Leftrightarrow x(m^2+2-3m)=5\)
Để PT trên vô nghiệm thì \(m^2-3m+2=0\)
\(\Leftrightarrow (m-1)(m-2)=0\)
\(\Leftrightarrow \left[\begin{matrix} m=1\\ m=2\end{matrix}\right.\)
Vậy \(m\in\left\{1;2\right\}\)