Question

[Dương Tú Vân]

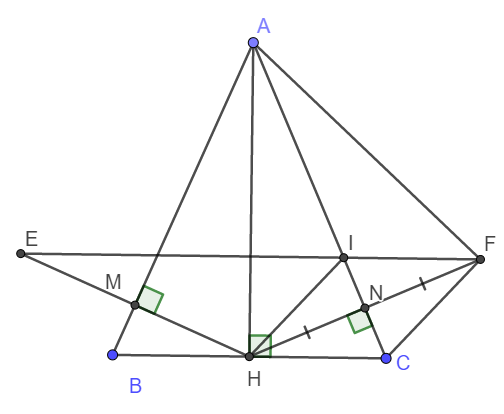
cho tam giác ABC cân tại A .Qua A kẻ đường thẳng vuông góc với BC gọi là AH. Kẻ HM vuông góc AB ,HN vuông góc AC .

a, Chứng minh : HM = HN

b, Trên tia đối của NH lấy F sao cho NF = NH. Chứng minh: FC vuông góc AF

c, Qua H kẻ đường thẳng song song FC cắt AC tại I. Chứng minh : IF song song BC

d, Trên tia đối của MH lấy E sao cho ME = MH. Chứng minh : E , I , F thẳng hàng

Answer 1

[nguyen thi vang]

a) Xét \(\Delta ABH,\Delta ACH\) có :

\(\widehat{ABH}=\widehat{ACH}\) (\(\Delta ABC\) cân tại A)

\(AB=AC\) (\(\Delta ABC\) cân tại A)

\(\widehat{AHB}=\widehat{AHC}\left(=90^o\right)\)

=> \(\Delta ABH=\Delta ACH\) (cạnh huyền - góc nhọn)

=> HB= HC (2 cạnh tương ứng)

Xét \(\Delta MBH,\Delta NCH\) có :

\(\widehat{MBH}=\widehat{KCH}\) (\(\Delta ABC\) cân tại A)

\(BH=CH\left(cmt\right)\)

\(\widehat{BMH}=\widehat{CNH}\left(=90^o\right)\)

=> \(\Delta MBH=\Delta NCH\) (cạnh huyền - góc nhọn)

=> HM = HN (2 cạnh tương ứng)

b) Xét \(\Delta AHN,\Delta AHF\) có :

\(NH=FN\left(gt\right)\)

\(\widehat{ANH}=\widehat{ANF}\left(=90^o\right)\)

\(AN:Chung\)

=> \(\Delta AHN=\Delta AHF\left(c.g.c\right)\)

Xét \(\Delta HNC,\Delta FNC\) có :

\(\widehat{HNC}=\widehat{FNC}\left(=90^o\right)\)

\(NC:Chung\)

\(HN=FN\left(gt\right)\)

=> \(\Delta HNC=\Delta FNC\left(c.g.c\right)\)

Ta có : \(\widehat{AHN}+\widehat{NHC}=90^o\)

Mà : \(\left\{{}\begin{matrix}\widehat{AHN}=\widehat{AKN}\\\widehat{NHC}=\widehat{NFC}\end{matrix}\right.\)

Nên : \(\widehat{AFN}+\widehat{NFC}=90^o\)

Hay : \(\widehat{AFC}=90^o\)

\(\Leftrightarrow FC\perp AF\)