giải hệ phương trình [x+y]√[x-y]+[x-y+1]√[x]=9
x2 +2X+4√[x2 -xy]=xy+y+17
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
0
CM
21 tháng 4 2019
Điều kiện: xy > 0
2 x 2 + y 2 + 2 x y = 16 x + y + 2 x y = 16 ⇔ 2 x 2 + y 2 = x + y ⇔ ( x – y ) 2 = 0 ⇔ x = y
Thay x = y vào x + y + x y = 16 ta được
2x + 2|x| = 16 ⇔ x + |x| = 8 ⇒ x = 4 ⇒ y = x = 4
Vậy hệ có một cặp nghiệm duy nhất (x; y) = (4; 4)
Khi đó x y = 4 4 = 1
Đáp án:D
CM
29 tháng 4 2018
Đáp án A
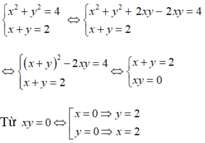
Vậy hệ phương trình có hai nghiệm (x; y) = (0; 2); (x; y) = (2; 0) Từ giả thiết x > y nên x = 2; y = 0 ⇒ xy = 0
V
0
29 tháng 12 2019
\(\hept{\begin{cases}x^2+y+x^3y+xy^2+xy=\frac{-5}{4}\\x^4+y^2+xy\left(1+2x\right)=\frac{-5}{4}\end{cases}}\)
29 tháng 12 2019
\(\Leftrightarrow\hept{\begin{cases}x^2+y+x^3y+xy^2+xy=\frac{-5}{4}\\x^4+2x^2y+y^2+xy=\frac{-5}{4}\end{cases}\Leftrightarrow\hept{\begin{cases}x^2+y+xy\left(x^2+y\right)+xy=\frac{-5}{4}\left(1\right)\\\left(x^2+y\right)^2+xy=\frac{-5}{4}\left(2\right)\end{cases}}}\)
Đặt x2 + y = a ; xy = b
Khi đó hệ phương trình trở thành : \(\hept{\begin{cases}a+ab+b=\frac{-5}{4}\\a^2+b=\frac{-5}{4}\end{cases}}\)\(\Leftrightarrow a+ab-a^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=0\\b-a+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x^2+y=0\\xy-\left(x^2+y\right)+1=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}y=-x^2\\x^2+y=xy+1\end{cases}}}\)
với y = -x2 thay vào ( 2 ), ta có : x . ( -x2 ) = \(\frac{-5}{4}\)\(\Rightarrow x=\sqrt[3]{\frac{5}{4}}\Rightarrow y=-\sqrt[3]{\frac{25}{16}}\)
với x2 + y = xy + 1 \(\Leftrightarrow\left(x^2-1\right)-\left(xy-y\right)=0\Leftrightarrow\left(x-1\right)\left(x+1-y\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x=y-1\end{cases}}\)từ đó suy ra \(y=\frac{-3}{2}\)
Vậy ....