cho tam giác abc d là trung điểm của ab .đường thẳng kẻ qua d và song song với cạnh bc cắt ac tại e.đường thẳng qua e và song song với cạnh ab cắt bc tại f. CMR
a.AD=EF
b.AE=EC
c.BF=FC
d.DE=1/2BC và EF =1/2 AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2022
a: Xét tứ giác BDEF có
DE//BF
BD//EF
Do đó: BDEF là hình bình hành
Suy ra: EF=BD
mà BD=AD
nên EF=AD
b: Xét ΔADF và ΔFEA có
AD=FE
AF chung
DF=EA
Do đó: ΔADF=ΔFEA
29 tháng 1 2023
a: Xét ΔABC có
D là trung điểm của AB
DE//BC
=>E là trung điểm của AC
=>AE=EC
Xét ΔCAB có
E là trung điểm của CA
EF//AB
=>F là trung điểm của BC
=>FB=FC
b: Xét ΔABC có D,E lần lượt là trung điểm của AB,AC
nên DE là đường trung bình
=>ED=1/2BC
Xét ΔCAB có CF/CB=CE/CA
nên EF//AB
=>FE/AB=CF/CB=1/2
=>FE=1/2AB
H
30 tháng 11 2014
D là TĐ của AB mà DE //BC nên DE là đg TB của tam giác ABC -->E là TĐ của AC.
E là TĐ của AC mà EF //AB nên EF là đg TB của tam giác CAB--->F là TĐ của BC
CH
Cô Hoàng Huyền
Admin
VIP
2 tháng 3 2018
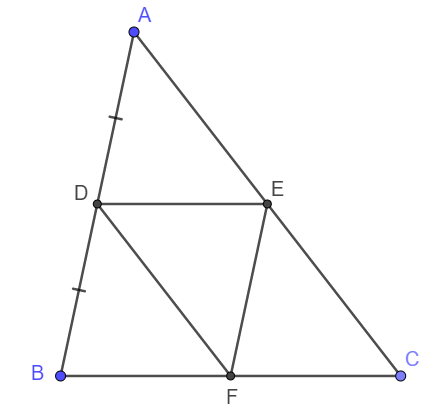
a) Xét tam giác DEF và tam giác FBD có:
Cạnh DF chung
\(\widehat{EDF}=\widehat{BFD}\) (Hai góc so le trong)
\(\widehat{EFD}=\widehat{BDF}\) (Hai góc so le trong)
\(\Rightarrow\Delta DEF=\Delta FBD\left(g-c-g\right)\Rightarrow EF=BD=AD\)
b)
Xét tam giác ADE và tam giác EFC có:
\(\widehat{DAE}=\widehat{FEC}\) (Hai góc so le trong)
\(\widehat{EFC}=\widehat{ADE}\left(=\widehat{DBF}\right)\)
\(\Rightarrow\Delta ADE=\Delta EFC\left(g-c-g\right)\Rightarrow AE=EC\)
Từ đó ta cũng suy ra DE = FC
Lại có do \(\Delta DEF=\Delta FBD\Rightarrow DE=FB\)
Vậy nên FC = FB
c) Ta có FC = FB = DE nên \(DE=\frac{BC}{2}\)
EF = AD = DB nên \(EF=\frac{AB}{2}\)
CM
19 tháng 4 2017
Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I
a: Xét tứ giác BDEF có
BD//EF
DE//BF
Do đó: BDEFlà hình bình hành
Suy ra: BD=EF=AD
b: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
hay AE=EC
c: Xét ΔABC có
E là trung điểm của AC
EF//AB
Do dó: F là trung điểm của BC
hay FB=FC
d: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
DO đó: DE là đường trung bình
=>DE=1/2BC