Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

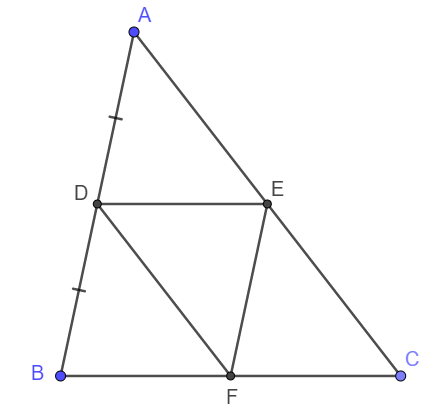
a) Xét tam giác DEF và tam giác FBD có:
Cạnh DF chung
\(\widehat{EDF}=\widehat{BFD}\) (Hai góc so le trong)
\(\widehat{EFD}=\widehat{BDF}\) (Hai góc so le trong)
\(\Rightarrow\Delta DEF=\Delta FBD\left(g-c-g\right)\Rightarrow EF=BD=AD\)
b)
Xét tam giác ADE và tam giác EFC có:
\(\widehat{DAE}=\widehat{FEC}\) (Hai góc so le trong)
\(\widehat{EFC}=\widehat{ADE}\left(=\widehat{DBF}\right)\)
\(\Rightarrow\Delta ADE=\Delta EFC\left(g-c-g\right)\Rightarrow AE=EC\)
Từ đó ta cũng suy ra DE = FC
Lại có do \(\Delta DEF=\Delta FBD\Rightarrow DE=FB\)
Vậy nên FC = FB
c) Ta có FC = FB = DE nên \(DE=\frac{BC}{2}\)
EF = AD = DB nên \(EF=\frac{AB}{2}\)

Bn ơi, cho mk hỏi tí! Cái chỗ góc A = góc DBM ( 2 góc tương ứng ) sao có thể suy ra AC // MB, bn có thể lm rõ hơn chỗ đó cho mk đc ko

Cứng đờ tay luôn rồi, khổ quá:((
a) Xét ΔDBFΔDBF và ΔFED:ΔFED:
DF:cạnh chung
ˆBDF=ˆEFDBDF^=EFD^(AB//EF)
ˆBFD=ˆEDFBFD^=EDF^(DE//BC)
=> ΔBDF=ΔEFD(g−c−g)ΔBDF=ΔEFD(g−c−g)
b) (Ở lớp 8 thì sé có cái đường trung bình ý bạn, nó sẽ có tính chất luôn, nhưng lớp 7 chưa học đành làm theo lớp 7 vậy)
Ta có: ˆDAE+ˆAED+ˆEDA=180oDAE^+AED^+EDA^=180o (Tổng 3 góc trong 1 tam giác)
Lại có: ˆAED+ˆDEF+ˆFEC=180oAED^+DEF^+FEC^=180o
Mà ˆDEF=ˆEDADEF^=EDA^(AB//EF)
=>ˆDAE=ˆFECDAE^=FEC^
Xét ΔDAEΔDAE và ΔFEC:ΔFEC:
DA=FE(=BD)
ˆDAE=ˆEFC(=ˆDBF)DAE^=EFC^(=DBF^)
ˆDAE=ˆFECDAE^=FEC^ (cmt)
=>ΔDAE=ΔFEC(g−c−g)ΔDAE=ΔFEC(g−c−g)
=> DE=FC(2 cạnh t/ứ)
=> Đpcm


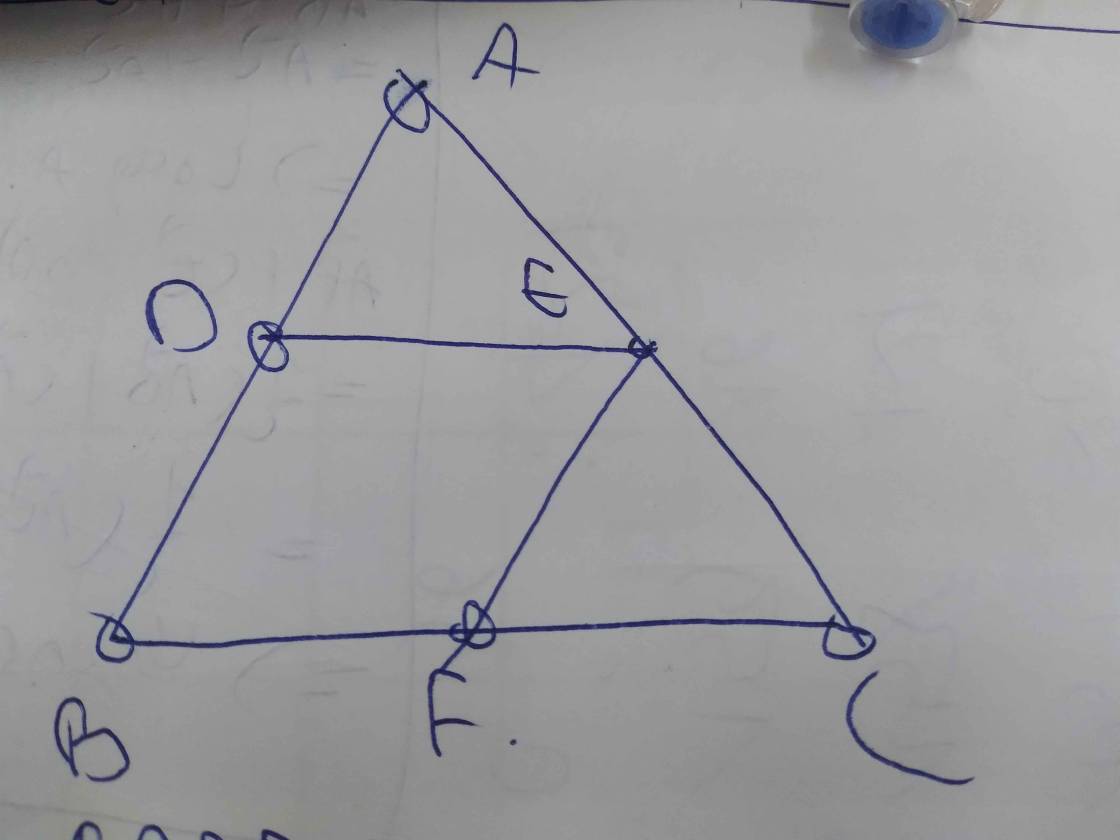


a: Xét ΔABC có
D là trung điểm của AB
DE//BC
=>E là trung điểm của AC
=>AE=EC
Xét ΔCAB có
E là trung điểm của CA
EF//AB
=>F là trung điểm của BC
=>FB=FC
b: Xét ΔABC có D,E lần lượt là trung điểm của AB,AC
nên DE là đường trung bình
=>ED=1/2BC
Xét ΔCAB có CF/CB=CE/CA
nên EF//AB
=>FE/AB=CF/CB=1/2
=>FE=1/2AB