Tính:
Giúp em phần b và phần h với ạ
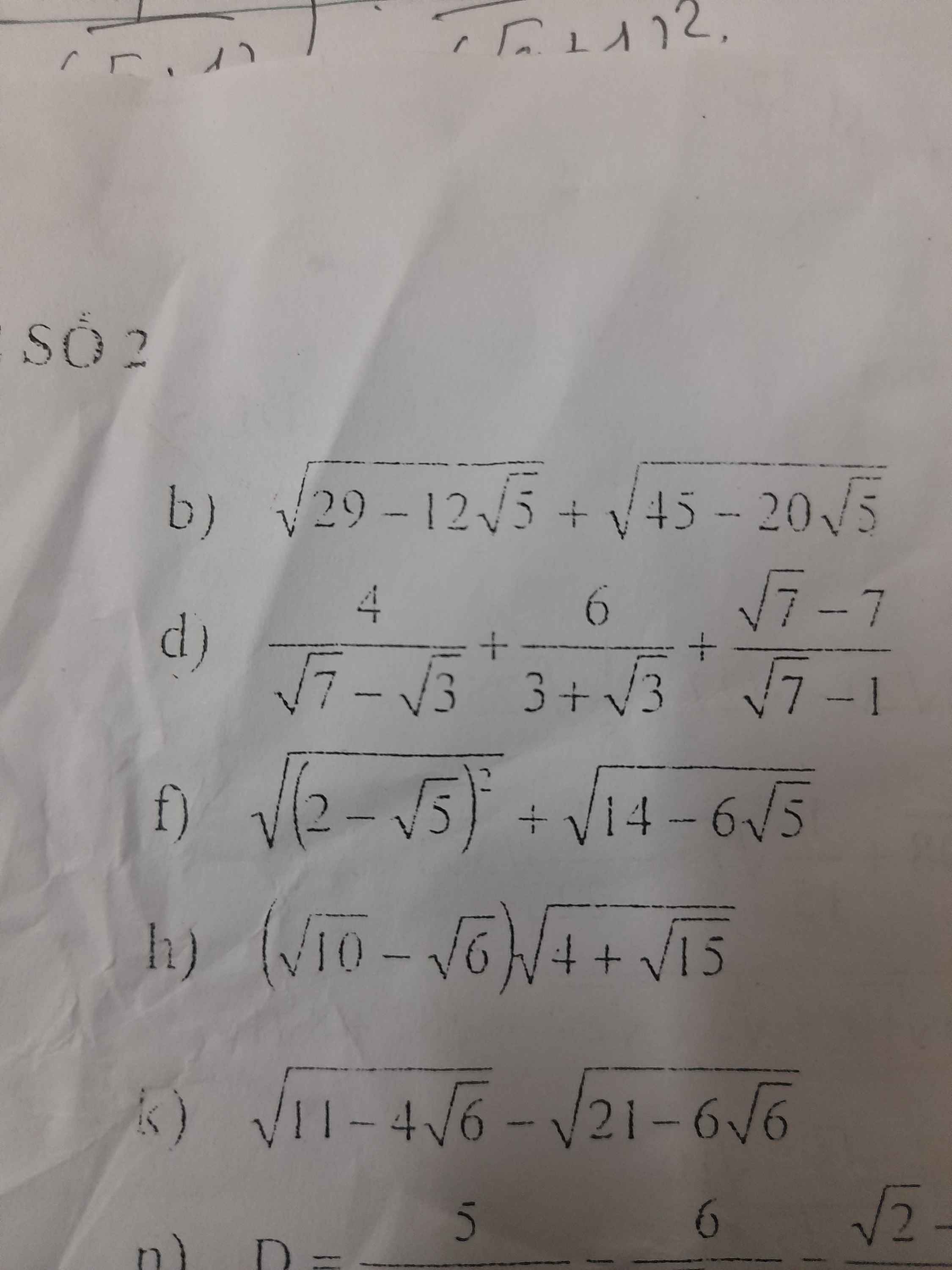
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{100\cdot101}\)
=1-1/2+1/2-1/3+...+1/100-1/101
=1-1/101=100/101
b: \(A=1+\dfrac{1}{2}+1+\dfrac{1}{6}+1+\dfrac{1}{12}+...+1+\dfrac{1}{10100}\)
\(=100+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{100}-\dfrac{1}{101}\right)\)
\(=101-\dfrac{1}{101}< 101\)

Bài 2:
b: Ta có: \(B=\dfrac{15-5\sqrt{x}}{x-5\sqrt{x}+6}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{-5\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-2}=1\)

ta có:
thời gian người đó đi trong nửa quãng đường đầu là:
t1\(=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{40}\left(1\right)\)
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S}{t_1+t_2+t_3}=\frac{S}{t_1+t'}\left(3\right)\)
ta lại có:
S2+S3=S/2
\(\Leftrightarrow v_2t_2+v_3t_3=\frac{S}{2}\)
\(\Leftrightarrow\frac{15t'}{2}+\frac{25t'}{2}=\frac{S}{2}\)
\(\Leftrightarrow40t'=S\Rightarrow t'=\frac{S}{40}\left(2\right)\)
thế (1) và (2) vào phương trình trên ta có:
\(v_{tb}=\frac{S}{\frac{S}{40}+\frac{S}{40}}=\frac{S}{S\left(\frac{2}{40}\right)}=\frac{1}{\frac{2}{40}}=20\)
quãng đường người đó đã đi là:
S=vtb.t=60km
vậy AB dài 60km

a, \(n_{CO_2}=\dfrac{17,6}{44}=0,4\left(mol\right)\)
CH4 + 2O2 -----to---> CO2 + 2H2O
x x
C2H4 + 3O2 -----to---> 2CO2 + 2H2O
y 2y
Ta có hệ pt: \(\left\{{}\begin{matrix}16x+28y=6\\x+2y=0,4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0,2\\y=0,1\end{matrix}\right.\)
\(\%m_{CH_4}=\dfrac{0,2.16.100\%}{6}=53,33\%;\%m_{C_2H_4}=100\%-53,33\%=46,67\%\)
b, \(\left\{{}\begin{matrix}\%V_{CH_4}=\dfrac{0,2.22,4.100\%}{\left(0,2+0,1\right).22,4}=66,67\%\\\%V_{C_2H_4}=100\%-66,67\%=33,33\%\end{matrix}\right.\)

He is widely regarded as the best man for the job.
The suspect could not account for the sand in his boots
sally came up with the best solution.
You need to make allowances for the fact that he hasn't spoken French for years.
It was inevitable that he would fail his exams.


b) \(\sqrt{29-12\sqrt{5}}+\sqrt{45-20\sqrt{5}}=\sqrt{\left(2\sqrt{5}-3\right)^2}+\sqrt{\left(5-2\sqrt{5}\right)^2}=2\sqrt{5}-3+5-2\sqrt{5}=2\)
h) \(\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4+\sqrt{15}}=\left(\sqrt{10}-\sqrt{6}\right)\sqrt{\left(\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{3}{2}}\right)^2}=\left(\sqrt{10}-\sqrt{6}\right)\left(\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{3}{2}}\right)=\sqrt{25}+\sqrt{15}-\sqrt{15}-\sqrt{9}=5-3=2\)
h: Ta có: \(\left(\sqrt{10}-\sqrt{6}\right)\cdot\sqrt{4+\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)\)
=5-3=2