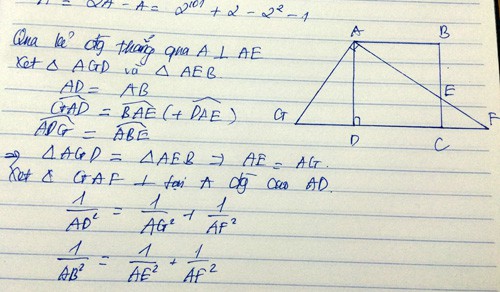cho hình vuông ABCD .Qua điểm A vẽ một đường thẳng cắt cạnh BC tại E và cắt đường thẳng CD tại F.CMR
\(\dfrac{1}{AB^2}=\dfrac{1}{AB^2}+\dfrac{1}{ÀF^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DD
Đâu Đủ Tư Cách
8 tháng 12 2017
Đúng(0)
Những câu hỏi liên quan
UV
26 tháng 12 2018
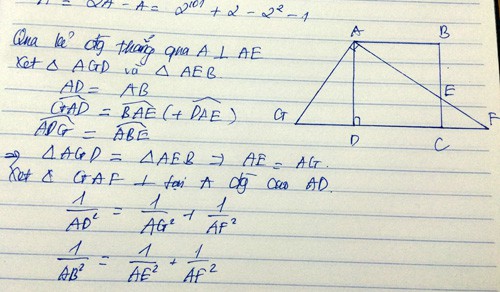
Kẻ AG⊥AF
Xét △ABE và △ADG có
\(\widehat{BAE}=\widehat{DAG}\) (cùng phụ góc DAF)
\(\widehat{ABE}=\widehat{ADG}=90^o\)
suy ra △ABE=△ADG
=> AE=AG(2 cạnh tương ứng)
Xét △AGF vuông tại A đường cao AD, Ta có:
\(\dfrac{1}{AD^2}=\dfrac{1}{AG^2}+\dfrac{1}{AF^2}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)
13 tháng 8 2023
b: Qua A kẻ đường thẳng vuông góc với AP cắt BC tại N
Xét ΔABN và ΔADP có
góc B=góc D=90 độ
góc BAN=góc DAP
=>ΔABN đồng dạng với ΔADP
=>AB/AD=AN/AP=1/3
=>AN=1/3AP
ΔANM vuông tại N có AB là đường cao
nen 1/AB^2=1/AM^2+1/AN^2=1/AM^2+9/AP^2
20 tháng 10 2023
Từ O kẻ đường thẳng song song với AB hay như nào vậy bạn.
16 tháng 9 2023
Xét hình thang ABCD có MN//AB//CD
nên AM/AD=BN/BC
Xét ΔADC có OM//DC
nên OM/DC=AM/AD
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC
=>OM/DC=ON/DC
=>OM=ON
=>O là trung điểm của MN
Xét ΔDAB có OM//AB
nên OM/AB=DM/DA
OM/AB+OM/DC
=AM/AD+ON/DC
=AM/AD+BN/BC
=1
=>1/AB+1/DC=1/OM=2/MN
24 tháng 2 2022
a: Xét hình thang ABCD có MN//AB//CD
nên AM/MN=BN/NC
=>AM/AD=BN/BC(1)
Xét ΔADC có MO//DC
nên MO/DC=AM/AB(2)
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC(3)
Từ (1), (2) và (3) suy ra MO=ON(đpcm)
b:
Để \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{MN}\) thì \(\dfrac{MN}{AB}+\dfrac{MN}{CD}=2\)
MN=2ON=2OM
\(\dfrac{2OM}{AB}+\dfrac{2ON}{CD}=2\left(\dfrac{OM}{AB}+\dfrac{ON}{CD}\right)\)
mà OM/AB=DO/DB
và ON/CD=BO/BD
nên \(VT=2\cdot\left(\dfrac{DO}{DB}+\dfrac{BO}{DB}\right)=2\left(đpcm\right)\)
6 tháng 11 2023
a: \(\widehat{ADE}+\widehat{EDC}=90^0\)
\(\widehat{KDC}+\widehat{EDC}=90^0\)
Do đó: \(\widehat{ADE}=\widehat{KDC}\)
Xét ΔADE vuông tại A và ΔCDK vuông tại C có
DA=DC
\(\widehat{ADE}=\widehat{KDC}\)
Do đó: ΔADE=ΔCDK
=>DE=DK
Xét ΔDEK có
\(\widehat{EDK}=90^0\)
DE=DK
Do đó: ΔDEK vuông cân tại D
b: Xét ΔDFK vuông tại D có DC là đường cao
nên \(\dfrac{1}{DK^2}+\dfrac{1}{DF^2}=\dfrac{1}{DC^2}\)
=>\(\dfrac{1}{DE^2}+\dfrac{1}{DF^2}=\dfrac{1}{DC^2}\) không đổi