Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Ta có:
ED,EAED,EA là tiếp tuyến của (O)
→ED⊥OD,EA⊥OA⇒ˆADE=ˆOAE=90o→ED⊥OD,EA⊥OA⇒ADE^=OAE^=90o
EDOAEDOA có ˆADE+ˆOAE=180oADE^+OAE^=180o
⇒EDOA⇒EDOA nội tiếp đường tròn đường kính (OE)
→ˆDOA+ˆDEA=180o→DOA^+DEA^=180o
Mà ABCDABCD là hình thang cân
→ˆDMA=ˆDBA+ˆCAB=2ˆDBA=ˆDOA→DMA^=DBA^+CAB^=2DBA^=DOA^
→ˆDMA+ˆAED=180o→AEDM→DMA^+AED^=180o→AEDM nội tiếp được trong một đường tròn
2. Từ câu 1
→ˆEMA=ˆEDA=ˆDBA=ˆCAB→EMA^=EDA^=DBA^=CAB^
Vì EDED là tiếp tuyến của (O),ABCDABCD là hình thang cân
→EM//AB→EM//AB
3. Ta có:
EM//AB→HK//AB→HMAB=DMDB=CMCA=MKABEM//AB→HK//AB→HMAB=DMDB=CMCA=MKAB
→MH=MK→M→MH=MK→M là trung điểm HK


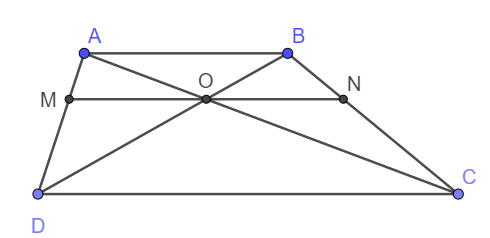
a) Do AB//CD nên áp dụng hệ quả định lý Ta let ta có:
\(\frac{AO}{OC}=\frac{OB}{OD}\) hay \(\frac{DO}{DB}=\frac{OC}{AC}\)
Xét tam giác ABD có OM//AB nên \(\frac{OM}{AB}=\frac{DO}{DB}\)
Tương tự \(\frac{ON}{AB}=\frac{CO}{CA}\)
Vậy nên \(\frac{OM}{AB}=\frac{ON}{AB}\Rightarrow OM=ON\)
b) Coi AB = 1, DC = k thì \(\frac{DO}{OB}=\frac{DC}{AB}=k\Rightarrow\frac{DO}{DB}=\frac{k}{k+1}\)
\(\Rightarrow OM=ON=\frac{k}{k+1}\Rightarrow MN=\frac{2k}{k+1}\)
Ta có \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{1}+\frac{1}{k}=\frac{k+1}{k}\)
\(\frac{2}{MN}=\frac{2}{\frac{2k}{k+1}}=\frac{k+1}{k}\)
Vậy nên \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{MN}\)
c) Ta thấy ngay \(\Delta COD\sim\Delta AOB\left(g-g\right)\) theo tỉ lệ k ở câu b.
Vậy thì \(\frac{S_{COD}}{S_{AOB}}=\frac{2009^2}{2008^2}=\left(\frac{2009}{2008}\right)^2=k^2\Rightarrow k=\frac{2009}{2008}\)
Từ đó ta có \(\frac{OC}{OA}=\frac{DO}{OB}=\frac{2009}{2008}\)
Vậy thì \(\frac{S_{ADO}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{ADO}=\frac{2009}{2008}.2008^2=2009.2008\)
\(\frac{S_{BOC}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{BOC}=\frac{2009}{2008}.2008^2=2009.2008\)
Suy ra \(S_{ABCD}=S_{AOB}+S_{DOC}+S_{AOD}+S_{BOC}=2008^2+2009^2+2.2008.2009\)
\(=\left(2008+2009\right)^2=4017^2\left(cm^2\right)\)

Từ O kẻ đường thẳng song song với AB hay như nào vậy bạn.

A B C D O a^2 b^2 M N
(Hình ảnh chỉ mang tính chất minh họa)
a) Kẻ DM và CN vuông góc với AB
=> MN = CD (Theo cách vẽ)
=> DC - AB = MN - AB = MA + BN
=> DC - AB = MA + BN
Tam giác vuông MAD và NBC vuông lần lượt tại M,N
=> AM < AD và BN < BC (Cạnh góc vuông < Cạnh huyền)
=> DC - AB = MA + BN < AD + BC (ĐPCM

Xét ΔADC có OM//DC
nên OM/DC=AM/AD
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC
Xét hình thang ABCD có MN//AB//CD
nên AM/AD=BN/BC
=>OM/DC=ON/DC
=>OM=ON
=>MN=2OM
OM//AB
=>OM/AB=DM/DA
OM//DC
=>OM/DC=AM/AD
=>OM/DC+OM/AB=DM/DA+AM/AD=1
=>1/AB+1/CD=1/OM
mà OM=1/2MN
nên 1/AB+1/CD=2/MN
Xét hình thang ABCD có MN//AB//CD
nên AM/AD=BN/BC
Xét ΔADC có OM//DC
nên OM/DC=AM/AD
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC
=>OM/DC=ON/DC
=>OM=ON
=>O là trung điểm của MN
Xét ΔDAB có OM//AB
nên OM/AB=DM/DA
OM/AB+OM/DC
=AM/AD+ON/DC
=AM/AD+BN/BC
=1
=>1/AB+1/DC=1/OM=2/MN