Cho tam giác ABC nhọn có BE và CF là hai đường cao. Kẻ EM và FN là hai dường cao của tam giác AED. Chứng minh MN//BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 1 2023
Xét tứ giác BFEC co góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
Xét tứ giác MNEF có goc FME=góc FNE=90 độ
nên MNEF là tứ giác nội tiếp
=>góc AMN=góc AEF=góc ABC
=>MN//BC
AH
Akai Haruma
Giáo viên
29 tháng 12 2017
Lời giải:
Xét tam giác $AFN$ và $AEM$ có:
\(\left\{\begin{matrix} \angle ANF=\angle AME=90^0\\ \angle A-\text{chung}\end{matrix}\right.\)
\(\Rightarrow \triangle AFN\sim AEM(g.g)\)
\(\Rightarrow \frac{AF}{AE}=\frac{AN}{AM}\)
Xét tam giác $AMN$ và $AEF$ có:
\(\left\{\begin{matrix} \frac{AN}{AM}=\frac{AF}{AE}\\ \angle A- \text{chung}\end{matrix}\right.\)
\(\Rightarrow \triangle AMN\sim \triangle AEF(c.g.c)\Rightarrow \angle AMN=\angle AEF(1)\)
Hoàn toàn tương tự, ta dễ dàng chứng minh được:
\(\triangle ABE\sim \triangle ACF(g.g)\Rightarrow \frac{AB}{AC}=\frac{AE}{AF}\)
Xét tam giác $AEF$ và tam giác $ABC$ có:
\(\left\{\begin{matrix} \angle A-\text{chung}\\ \frac{AE}{AF}=\frac{AB}{AC}\end{matrix}\right.\)
\(\Rightarrow \triangle AEF\sim \triangle ABC(c.g.c)\Rightarrow \angle AEF=\angle ABC(2)\)
Từ (1),(2) suy ra \(\angle AMN=\angle ABC\)
Mà hai góc này ở vị trí đồng vị nên \(MN\parallel BC\)
Ta có đpcm.
18 tháng 5 2022
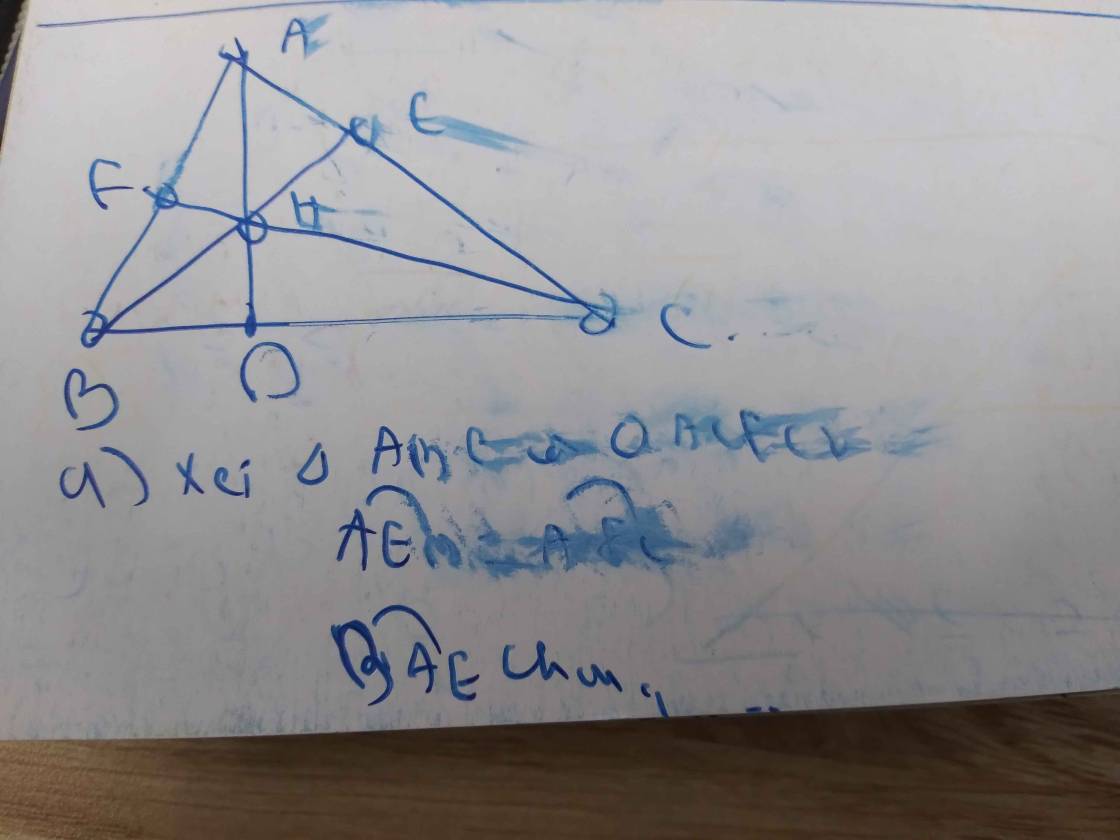
a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{FEC}+\widehat{ABC}=180^0\)
26 tháng 3 2021
a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
