Cho 2 dường tròn (O1,5cm) và (O2,2cm) nằm ngoài nhau. 1 tiếp tuyền chung ngoài AB của 2 đường tròn, \(A\in(O_1),B\in\left(O_2\right)\) và 1 tiếp tuyến chung trong CD của 2 đường tròn, \(C\in\left(O_1\right),D\in\left(O_2\right)\). Tính độ dài đoạn nối tâm O1O2 biết AB=1,5 CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
18 tháng 9 2017
Gọi giao điểm của O1O2 và CD là I.
Ta thấy rằng \(\Delta O_1CI\sim\Delta O_2DI\) theo tỉ số đồng dạng là \(k=\frac{O_1C}{O_2D}=\frac{5}{2}\)
Đặt \(ID=2x\left(cm\right)\Rightarrow IC=5x\Rightarrow CD=7x\Rightarrow AB=1,5.7x=10,5x\)
Theo Pitago ta cũng có \(O_1I=\sqrt{25x^2+25};O_2I=\sqrt{4x^2+4}\left(1\right)\)
Xét hình thang vuông ABO2O1 , kẻ O2H vuông góc với AO1 , ta tính được \(HO_1=5-2=3\left(cm\right)\)
Vậy thì \(O_1O_2^2=O_2H^2+HO_1^2\Rightarrow O_1O_2=\sqrt{110,25x^2+9}\left(2\right)\)
Từ (1) và (2) suy ra \(\sqrt{110,25x^2+9}=\sqrt{25x^2+25}+\sqrt{4x^2+4}\)
\(\Leftrightarrow\sqrt{110,25x^2+9}=5\sqrt{x^2+1}+2\sqrt{x^2+1}\)
\(\Leftrightarrow\sqrt{110,25x^2+9}=7\sqrt{x^2+1}\)
\(\Leftrightarrow110,25x^2+9=49x^2+49\)
\(\Leftrightarrow x^2=\frac{32}{49}\Rightarrow O_1O_2=7.\sqrt{\frac{32}{49}+1}=9\left(cm\right)\)
Vậy O1O2 = 9 cm.
5 tháng 11 2016
Từ O1 kẻ O1H vuông góc với O2C tại H. Vì R2 > R1 nên ta được O1BCH là hình chữ nhật
và : O2H = R2 - R1 = 2
\(cos\widehat{O_1O_2H}=\frac{O_2H}{O_1O_2}=\frac{2}{8}=\frac{1}{4}\Rightarrow\widehat{O_1O_2H}=\alpha\)(Bạn bấm máy tính để tìm giá trị góc này, còn mình đặt là \(\alpha\)cho dễ nhìn)
\(\Rightarrow\widehat{BO_1O_2}=180^o-\alpha\)(BO1 // CO2)
\(AB=\sqrt{2R^2_1-2R_1^2.cos\left(180^o-\alpha\right)}=m\)
\(AC=\sqrt{2R_2^2-2R_2^2.cos\alpha}=n\)
Gọi \(S_1\) và \(S_2\) lần lượt là diện tích hình quạt \(O_1AB\) và \(O_2AC\) thì ta có :
\(S_1=\frac{\pi.R_1^2.\left(180^o-\alpha\right)}{360^o}\) ; \(S_2=\frac{\pi.R_2^2.\alpha}{360^o}\)
\(S_{\Delta O_1AB}=\frac{1}{2}.R_1^2.sin\left(90^o-\alpha\right)\); \(S_{\Delta O_2AC}=\frac{1}{2}R_2^2.sin\alpha\)
Diện tích hình viên phân giới hạn bởi AB là : \(S'=S_1-S_{\Delta O_1AB}=x\)
Diện tích hình viên phân giới hạn bởi AC là : \(S''=S_2-S_{\Delta O_2AC}=y\)
Diện tích tam giác ABC nằm ngoài cả hai đường tròn đã cho là :
\(S_{ABC}-S'-S''=\frac{1}{2}m.n-x-y\)
LV
6 tháng 5 2017
a) kéo dài O1E,O2F cắt CD ở M và N
b) góc BFI + góc BEI =180
c) gọi AB cắt EF ở K
bằng đồng dạng ta chứng minh được KE=KF=KB.KA(đpcm)
2 tháng 1
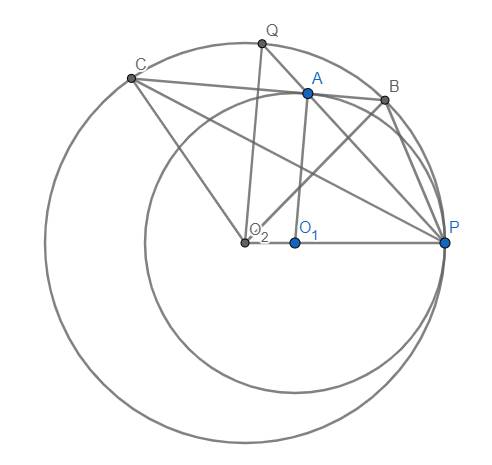
Gọi Q là giao điểm của PA và (O2). Do \(\widehat{O_1AP}=\widehat{O_1PA}=\widehat{O_2PQ}=\widehat{O_2QP}\) nên O1A//O2Q
Mặt khác, \(BC\perp O_1A\) (vì BC là tiếp tuyến tại A của (O1) nên \(BC\perp O_2Q\)
\(\Rightarrow\) Q là điểm chính giữa của cung nhỏ BC
\(\Rightarrow\) PQ là tia phân giác \(\widehat{BPC}\) \(\Rightarrow\) đpcm
NN
21 tháng 2 2022
a) Vì AH, HB, AB đều là các đường kính của các nửa đường tròn (O1) , (O2) và (O) nên tứ giác MPHQ có ba góc P, Q, M vuông. Vì vậy nó là hình chữ nhật.
Từ đó, ta có HM = PQ.
b) Vì MHPQ là hình chữ nhật nên , do đó APQB là tứ giác nội tiếp.
c) Ta có
nên PQ tiếp xúc nửa đường tròn (O1) tại P.
Tương tự , PQ tiếp xúc (O2) tại Q hay PQ là tiếp tuyến chung của hai nửa đường tròn (O1) và (O2)
15 tháng 12 2021
ta có : Góc CAB = GÓc PQG ( 2 góc đối đỉnh ) . theo tính chất của góc nt , taco : Góc CBA = 1/2 cung AC . Góc APQ = 1/2 sd AQ(1) . theo t/c của góc tạo bởi tia tiếp tuyến và dây cung ta có ; GÓC CBA = 1/2 cung AC . APQ + 1/2 sđ AQ ( 2) . TỪ (1) , ( 2 ) => GÓC CBA = APQ . mà 2 góc này ở vị trí soletrong = > BC song song với QP
15 tháng 12 2021
xAC=QAy(hai góc đối đỉnh)
theo tính chất của 2 góc được tạo bởi tia tiếp tuyến
=> xAC=1/2sđ cung AC,QAy=1/2sđ cungAQ(1)
theo tính chất của góc nội tiếp,ta có
=> ABC=1/2 sđ cung AC,APQ=1/2sđ cung AQ(2)
từ (1),(2)=> ABC=APQ
=> QP//BC
