Tìm x biết 10x2 -19x = 33
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
\(\begin{array}{l}a){\rm{ }}3{x^2}-{\rm{ }}3x\left( {x{\rm{ }}-{\rm{ }}2} \right){\rm{ }} = {\rm{ }}36\\ \Leftrightarrow 3{x^2}-{\rm{ [}}3x.x + 3x.( - 2)] = 36\\ \Leftrightarrow 3{x^2} - (3{x^2} - 6x) = 36\\ \Leftrightarrow 3{x^2} - 3{x^2} + 6x = 36\\ \Leftrightarrow 6x = 36\\ \Leftrightarrow x = 36:6\\ \Leftrightarrow x = 6\end{array}\)
Vậy x = 6
\(\begin{array}{l}b){\rm{ }}5x\left( {4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}-{\rm{ }}2x\left( {10{x^2}-{\rm{ }}5x{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }} - 36\\ \Leftrightarrow 5x.4{x^2} + 5x.( - 2x) + 5x.1 - [2x.10{x^2} + 2x.( - 5x) + 2x.2] = - 36\\ \Leftrightarrow 20{x^3} - 10{x^2} + 5x - (20{x^3} - 10{x^2} + 4x) = - 36\\ \Leftrightarrow 20{x^3} - 10{x^2} + 5x - 20{x^3} + 10{x^2} - 4x = - 36\\ \Leftrightarrow (20{x^3} - 20{x^3}) + ( - 10{x^2} + 10{x^2}) + (5x - 4x) = - 36\\ \Leftrightarrow x = - 36\end{array}\)
Vậy x = -36
23 tháng 1 2017
\(x+3+7x-19x=38\)
\(-11x+3=38\)
\(-11x=38-3\)
\(-11x=35\)
\(x=-\frac{35}{11}\)
NT
8
30 tháng 7 2015
( 19x + 2.52 ) : 14 = ( 13 - 8 )2- 4 2
( 19x + 2.52 ) : 14 = 52- 4 2
( 19x + 2.52 ) : 14 = 25- 16
( 19x + 2.52 ) : 14 =9
( 19x + 50 ) : 14 =9
19x + 50=9 . 14
19x + 50=126
19x=126-50
19x=76
x=76:19
x=4
NK
0
NV
0
PT
1
CM
20 tháng 3 2018
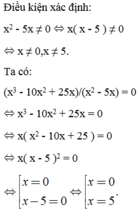
So sánh điều kiện, không có giá trị nào của x thỏa mãn.
Vậy không có giá trị x nào thỏa mãn yêu cầu đề bài.
\(10x^2-19x=33\)
\(\Rightarrow10x^2-19x-33=0\)
\(\Rightarrow10x^2-30x+11x-33=0\)
\(\Rightarrow10x\left(x-3\right)+11\left(x-3\right)=0\)
\(\Rightarrow\left(x-3\right)\left(10x+11\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\10x+11=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=3\\10x=-11\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-1,1\end{matrix}\right.\)
Vậy..............
\(10x^2-19x=33\)
\(\Leftrightarrow10x^2-19x-33=0\)
\(\Leftrightarrow10x^2-30x+11x-33=0\)
\(\Leftrightarrow10x\left(x-3\right)+11\left(x-3\right)=0\)
\(\Leftrightarrow\left(10x+11\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}10x+11=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-11}{10}\\x=3\end{matrix}\right.\)
Vậy \(x=\dfrac{-11}{10}\) hoặc x = 3