
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




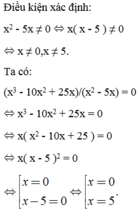
So sánh điều kiện, không có giá trị nào của x thỏa mãn.
Vậy không có giá trị x nào thỏa mãn yêu cầu đề bài.

\(x^3-19x=0\)
\(x\left(x^2-19\right)=0\)
\(\orbr{\begin{cases}x=0\\x^2-19=0\end{cases}\orbr{\begin{cases}x=0\\x^2=19\end{cases}\orbr{\begin{cases}x=0\left(TM\right)\\x=\sqrt{19}\left(TM\right)\end{cases}}}}\)

Để \(A⋮B\) thì \(10x^2-7x-5⋮2x-3\)
\(\Leftrightarrow10x^2-15x+8x-12+7⋮2x-3\)
\(\Leftrightarrow5x\left(2x-3\right)+4\left(2x-3\right)+7⋮2x-3\)
\(\Leftrightarrow\left(2x-3\right)\left(5x+4\right)+7⋮2x-3\)
mà \(\left(2x-3\right)\left(5x+4\right)⋮2x-3\)
nên \(7⋮2x-3\)
\(\Leftrightarrow2x-3\inƯ\left(7\right)\)
\(\Leftrightarrow2x-3\in\left\{1;-1;7;-7\right\}\)
\(\Leftrightarrow2x\in\left\{4;2;10;-4\right\}\)
hay \(x\in\left\{2;1;5;-2\right\}\)(nhận)
Vậy: Khi \(x\in\left\{2;1;5;-2\right\}\) thì \(A⋮B\)
Điều kiện: \(B\ne0\Leftrightarrow2x-3\ne0\Leftrightarrow x\ne\dfrac{3}{2}\).
Ta có: \(\dfrac{A}{B}=\dfrac{10x^2-7x-5}{2x-3}=\dfrac{10x^2-15x+8x-12+7}{2x-3}\\ =\dfrac{5x\left(2x-3\right)+4\left(2x-3\right)+7}{2x-3}=5x+4+\dfrac{7}{2x-3}\)
Để \(A⋮B\) thì \(\left(2x-3\right)\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
Nếu \(2x-3=1\Leftrightarrow2x=4\Leftrightarrow x=2\) (Thỏa mãn)
Nếu \(2x-3=-1\Leftrightarrow2x=2\Leftrightarrow x=1\) (Thỏa mãn)
Nếu \(2x-3=7\Leftrightarrow2x=10\Leftrightarrow x=5\) (Thỏa mãn)
Nếu \(2x-3=-7\Leftrightarrow2x=-4\Leftrightarrow x=-2\) (Thỏa mãn).
Vậy tập các giá trị \(x\) thỏa mãn là \(\left\{1;\pm2;5\right\}\).

Bài 3:
b. $B=(x+y)(2x-y)+(xy^4-x^2y^2):(xy^2)$
$=(2x^2-xy+2xy-y^2)+(y^2-x)$
$=2x^2+xy-y^2+y^2-x=2x^2+xy-x$
Bài 4:
a. $25x^3-10x^2+x=x(25x^2-10x+1)=x(5x-1)^2$
b. $x^2-9x+9y-y^2=(x^2-y^2)-(9x-9y)=(x-y)(x+y)-9(x-y)=(x-y)(x+y-9)$
c. $16-x^2-4y^2-4xy=16-(x^2+4y^2+4xy)$
$=4^2-(x+2y)^2=(4-x-2y)(4+x+2y)$

b) Vậy C = 2 ⇒ (2/x) = 2
⇒ x = 1(thỏa mãn các điều kiện trên).
\(10x^2-19x=33\)
\(\Rightarrow10x^2-19x-33=0\)
\(\Rightarrow10x^2-30x+11x-33=0\)
\(\Rightarrow10x\left(x-3\right)+11\left(x-3\right)=0\)
\(\Rightarrow\left(x-3\right)\left(10x+11\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\10x+11=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=3\\10x=-11\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-1,1\end{matrix}\right.\)
Vậy..............
\(10x^2-19x=33\)
\(\Leftrightarrow10x^2-19x-33=0\)
\(\Leftrightarrow10x^2-30x+11x-33=0\)
\(\Leftrightarrow10x\left(x-3\right)+11\left(x-3\right)=0\)
\(\Leftrightarrow\left(10x+11\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}10x+11=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-11}{10}\\x=3\end{matrix}\right.\)
Vậy \(x=\dfrac{-11}{10}\) hoặc x = 3