Cho hai đường tròn (O) và (O') cắt nhau tại A và B như hình 77. Biết OA = 15cm, O'A = 13 cm, AB = 24cm. Tính độ dài OO' ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
23 tháng 6 2017
Đúng(0)
Những câu hỏi liên quan
CM
12 tháng 7 2018
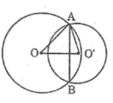
Gọi H là giao điểm của AB và OO’.
Vì OO’ là đường trung trực của AB nên:
OO’ ⊥ AB tại H
Suy ra: HA = HB = (1/2).AB = (1/2).24 = 12 (cm)
Áp dụng định lí Pitago vào tam giác vuông AOH, ta có:
A O 2 = O H 2 + A H 2
Suy ra: O H 2 = O A 2 - A H 2 = 15 2 - 12 2 = 81
OH = 9 (cm)
Áp dụng định lí pitago vào tam giác vuông AO’H, ta có:
A O ' 2 = O H ' 2 + A H 2
Suy ra: O ' H 2 = O ' A 2 - A H 2 = 13 2 - 12 2 = 25
O’H = 5 (cm)
Vậy OO’ = OH + O’H = 9 + 5 = 14 (cm)
CM
24 tháng 10 2019
Gọi I là trung điểm AB. Chú ý 1 A I 2 + 1 O A 2 + 1 O ' A 2
Ta tính được AB=24cm
HH
16 tháng 11 2020
- Trường hợp 1: O và O' nằm khác phía đối với AB
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có
\(AB\perp OO'\) ; AI = IB = 12
Áp dụng định lí Pitago , ta được :
\(OI=\sqrt{OA^2-AI^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\left(cm\right)\)
\(IO'=\sqrt{O'A^2-AI^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\left(cm\right)\)
Vậy OO' = OI + IO' = 16 + 9 = 25 ( cm )
- Trường hợp 2: O và O' nằm cùng phía đối với AB
Như TH1 , ta lại có :
\(OI=\sqrt{OA^2-AI^2}=16\left(cm\right)\)
\(O'I=\sqrt{O'A^2-AI^2}=9\left(cm\right)\)
Vậy OO' = OI – O'I = 16 – 9 = 7 ( cm )
KD
25 tháng 4 2017
a) Trường hợp O và O’ nằm khác phía đối với AB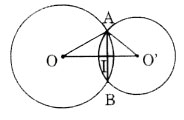
Ta có: AI =1/2 AB = 12
OI2 = OA2 – AI2
=400-144 =256
⇒ OI =16
O’I2 = O’A2 – AI2 =255 -144 =81
⇒ O’I = 9
Ta có: OO’ = OI + OI’ = 16 + 9 =25 (cm).
b) Trường hợp O và O’ nằm cùng phía đối với AB.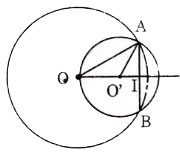
Ta có: OI2 = OA2 – AI2 = 256
⇒ OI =16
Tương tự O’I= 9
Do đó: OO’= OI – O’I =16 – 9= 7(cm)
7 tháng 1 2023
a: Xét (O;R) có
OA là bán kính
O'A vuông góp với OA
Do đó: O'A là tiếp tuyến của (O)
b: \(OO'=\sqrt{12^2+5^2}=13\left(cm\right)\)
AH=5*12/13=60/13(cm)
=>AB=120/13(cm)
7 tháng 1 2023
a: Xét (O;R) có
OA là bán kính
O'A vuông góp với OA
Do đó: O'A là tiếp tuyến của (O)
b: \(OO'=\sqrt{12^2+5^2}=13\left(cm\right)\)
AH=5*12/13=60/13(cm)
=>AB=120/13(cm)