Tìm tập hợp tất tả các điểm M trong không gian luôn luôn nhìn đoạn thẳng AB cố định dưới một góc vuông ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 4 2018
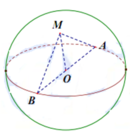
+ Gọi O là trung điểm của AB.
Tam giác AMB là vuông tại M có OM là đường trung tuyến ứng với cạnh huyền nên :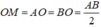 
Suy ra, M thuộc mặt cầu tâm O, bán kính là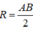 
+ Ngược lại, xét mặt cầu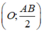 
với O là trung điểm của AB.
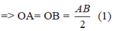
Lấy điểm M bất kì thuộc mặt cầu này. Suy ra: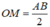 
(2)
Từ (1) và (2) suy ra:
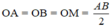
⇒ Tam giác MAB vuông tại M.
Kết luận: Vậy tập hợp các điểm M trong không gian luôn nhìn đoạn thẳng AB cố định dưới 1 góc vuông là mặt cầu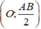 
CM
28 tháng 5 2018
Đáp án B
Gọi O là trung điểm của đoạn thẳng AB, ta có:
M / A M ⏜ B = 90 ° = M / OM = AB 2 = S O ; AB 2
Vậy tập hợp các điểm M nhìn đoạn thẳng cố định AB dưới một góc vuông là mặt cầu tâm O bán kính R = AB 2 .
CM
19 tháng 12 2017
Đáp án C
Cách giải:
M di động luôn nhìn đoạn AB dưới một góc vuông ⇒ M thuộc mặt cầu có một đường kính là AB.
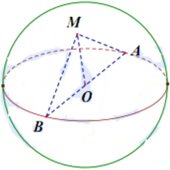
Gọi O là trung điểm đoạn thẳng AB, vì tam giác AMB vuông tại M nên trung tuyến MO bằng nửa cạnh huyến, tức MO = AB/2 = R.
Vậy tập hợp các điểm M nhìn AB dwói một góc vuông nằm trêm mặt càu đường kính AB
Ngược lại, lấy M thuốc mặt cầu đwòng kính AB thì MO = AB/2 do đó nếu M khác A và B thì tam giác MAB vuông tại M, còn khi M = A hoặc M = B ta cũng coi M nhìn AB một góc vuông.
Kết luận: Tập hợp các điểm M trong không gian nhín đoạn thẳng AB dưới một góc vuông là mặt cầu đương kính AB